東京工業大学2021年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 正の整数に関する条件
(*) 10進法で表したときに、どの位にも数字9が現れない
を考える。以下の問いに答えよ。
(1) kを正の整数とするとき、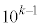 以上かつ
以上かつ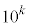 未満であって条件(*)を満たす正の整数の個数を
未満であって条件(*)を満たす正の整数の個数を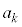 とする。このとき、
とする。このとき、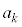 をkの式で表せ。
をkの式で表せ。 (2) 正の整数nに対して、
とおく。このとき、すべての正の整数kに対して次の不等式が成り立つことを示せ。
[解答へ]
[2] xy平面上の楕円
E: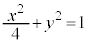
について、以下の問いに答えよ。
(1) a,bを実数とする。直線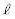 :
: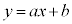 と楕円Eが異なる2点を共有するためのa,bの条件を求めよ。
と楕円Eが異なる2点を共有するためのa,bの条件を求めよ。 (2) 実数a,b,cに対して、直線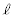 :
: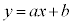 と直線m:
と直線m: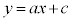 がそれぞれ楕円Eと異なる2点を共有しているとする。ただし、
がそれぞれ楕円Eと異なる2点を共有しているとする。ただし、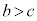 とする。直線
とする。直線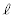 と楕円Eの2つの共有点のうちx座標の小さい方をP,大きい方をQとする。また、直線mと楕円Eの2つの共有点のうちx座標の小さい方をS,大きい方をRとする。このとき、等式
と楕円Eの2つの共有点のうちx座標の小さい方をP,大きい方をQとする。また、直線mと楕円Eの2つの共有点のうちx座標の小さい方をS,大きい方をRとする。このとき、等式 が成り立つためのa,b,cの条件を求めよ。
(3) 楕円E上の4点の組で、それらを4頂点とする四角形が正方形であるものをすべて求めよ。
[解答へ]
[3] 以下の問いに答えよ。
(1) 正の整数nに対して、二項係数に関する次の等式を示せ。
また、これを用いて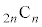 は
は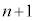 の倍数であることを示せ。
の倍数であることを示せ。 (2) 正の整数nに対して、
とおく。このとき、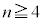 ならば
ならば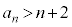 であることを示せ。
であることを示せ。 (3) 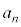 が素数となる正の整数nをすべて求めよ。
が素数となる正の整数nをすべて求めよ。 [解答へ]
[4] Sを、座標空間内の原点Oを中心とする半径1の球面とする。S上を動く点A,B,C,Dに対して
とおく。以下の問いに答えよ。
(1) 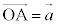 ,
,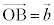 ,
,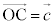 ,
,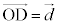 とするとき、
とするとき、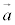 ,
,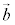 ,
,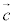 ,
,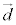 によらない定数kによって
によらない定数kによって と書けることを示し、定数kを求めよ。
(2) 点A,B,C,Dが球面S上を動くときの、Fの最大値Mを求めよ。
(3) 点Cの座標が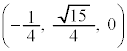 ,点Dの座標が
,点Dの座標が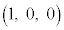 であるとき、
であるとき、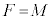 となるS上の点A,Bの組をすべて求めよ。
となるS上の点A,Bの組をすべて求めよ。 [解答へ]
[5] xy平面上の円C: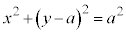
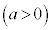 を考える。以下の問いに答えよ。
を考える。以下の問いに答えよ。
(1) 円Cが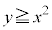 で表される領域に含まれるためのaの範囲を求めよ。
で表される領域に含まれるためのaの範囲を求めよ。 (2) 円Cが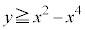 で表される領域に含まれるためのaの範囲を求めよ。
で表される領域に含まれるためのaの範囲を求めよ。 (3) aが(2)の範囲にあるとする。xy平面において連立不等式
で表される領域Dを、y軸の周りに1回転させてできる立体の体積を求めよ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東工大数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 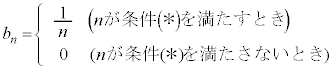
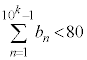
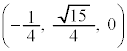 ,点Dの座標が
,点Dの座標が