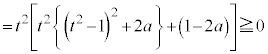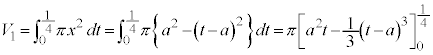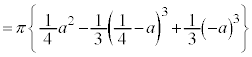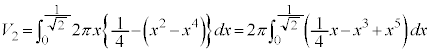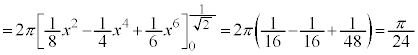���H�吔�w'21�N�O��[5]
xy���ʏ�̉~C�F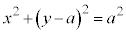
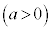 ���l����B�ȉ��̖₢�ɓ�����B
���l����B�ȉ��̖₢�ɓ�����B
(1) �~C��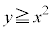 �ŕ\�����̈�Ɋ܂܂�邽�߂�a�͈̔͂����߂�B
�ŕ\�����̈�Ɋ܂܂�邽�߂�a�͈̔͂����߂�B (2) �~C��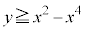 �ŕ\�����̈�Ɋ܂܂�邽�߂�a�͈̔͂����߂�B
�ŕ\�����̈�Ɋ܂܂�邽�߂�a�͈̔͂����߂�B (3) a��(2)�͈̔͂ɂ���Ƃ���Bxy���ʂɂ����ĘA���s����
�ŕ\�����̈�D���Ay���̎����1��]�����Ăł��闧�̂̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
��(1)��(2)�̃q���g�A�Ƃ����̂��o��҂̈Ӑ}���Ǝv���܂��B(2)�́A�������Ď�蓾��l�͈̔͂����߂�A�Ƃ����Œ�ϔO�ɂƂ���Ă��܂��Ƃ��܂������܂���B�Ȃ��A�~�ƕ������̈ʒu�W���Q�Ƃ��Ă��������B
(1) �~ C��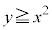 �ŕ\�����̈�Ɋ܂܂�邽�߂ɂ́A�Ȑ�
�ŕ\�����̈�Ɋ܂܂�邽�߂ɂ́A�Ȑ�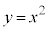 ��̂��ׂĂ̓_
��̂��ׂĂ̓_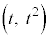 (t �͔C�ӂ̎���)�Ɖ~C�̒��S
(t �͔C�ӂ̎���)�Ɖ~C�̒��S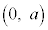 �Ƃ�������2�悪�~�̔��a��2��
�Ƃ�������2�悪�~�̔��a��2��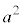 �ȏ�ł���悭�A
�ȏ�ł���悭�A ���ꂪ�A�C�ӂ̎���t �Ő��藧���߂ɂ́A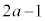 �͒萔��
�͒萔��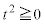 ���A
���A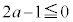 ���K�v�\���ł��B
���K�v�\���ł��B
����āA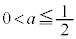 ......[��]
......[��] (2) �~C��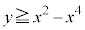 �ŕ\�����̈�Ɋ܂܂�邽�߂ɂ́A�Ȑ�
�ŕ\�����̈�Ɋ܂܂�邽�߂ɂ́A�Ȑ�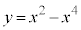 ��̂��ׂĂ̓_
��̂��ׂĂ̓_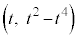 (t �͔C�ӂ̎���)�Ɖ~C�̒��S
(t �͔C�ӂ̎���)�Ɖ~C�̒��S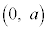 �Ƃ̋�����2�悪�~�̔��a��2��
�Ƃ̋�����2�悪�~�̔��a��2��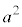 �ȏ�ł���悭�A
�ȏ�ł���悭�A ���ӂ���E�ӂ������ƁA
���ꂪ�C�ӂ̎���t �Ő��藧���߂ɂ́A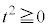 �C
�C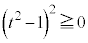 �C
�C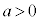 ���A
���A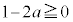 ���K�v�\���ŁA
���K�v�\���ŁA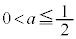 ......[��]
......[��] ���D�@�̒��J�b�R����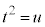 (
(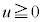 )�Ƃ����Ċ��F
)�Ƃ����Ċ��F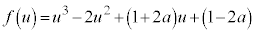 ���l���A�������A
���l���A�������A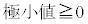 �Ɏ������ނƂ������j�͂��܂��s���܂���B
�Ɏ������ނƂ������j�͂��܂��s���܂���B (3) �Ȑ�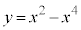 �́A
�́A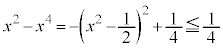 ���A
���A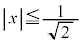 �܂�
�܂�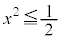 �ɂ����ẮA
�ɂ����ẮA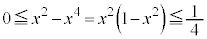 �ƂȂ�̂ŁA�Ȑ�
�ƂȂ�̂ŁA�Ȑ�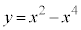 ��
��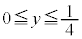 �͈̔͂ɑ��݂��܂��B
�͈̔͂ɑ��݂��܂��B (2)���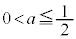 �ł����A
�ł����A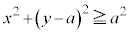 �̋��E��C�̕��́A�O���t��
�̋��E��C�̕��́A�O���t��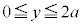 �͈̔͂ɂ���̂ŁA
�͈̔͂ɂ���̂ŁA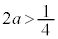 �C�܂�A
�C�܂�A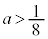 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A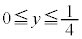 �͈̔͂���㑤�ɂ͂ݏo���܂��B�����ŁA
�͈̔͂���㑤�ɂ͂ݏo���܂��B�����ŁA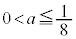 �̏ꍇ�ƁA
�̏ꍇ�ƁA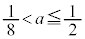 �̏ꍇ�ŁA�ꍇ�������K�v�ɂȂ�܂��B
�̏ꍇ�ŁA�ꍇ�������K�v�ɂȂ�܂��B �E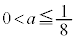 �̂Ƃ��A�~C�́A(2)�̌��ʂƍ��킹�āA
�̂Ƃ��A�~C�́A(2)�̌��ʂƍ��킹�āA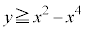 ����
����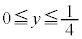 �͈̔͂Ɋ܂܂�A�~C��y���̎���ɉ�]�����Ăł���A���aa�̋��̑̐�
�͈̔͂Ɋ܂܂�A�~C��y���̎���ɉ�]�����Ăł���A���aa�̋��̑̐�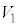 �́A
�́A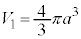
�E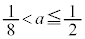 �̂Ƃ��ɂ́A�~C��
�̂Ƃ��ɂ́A�~C��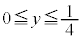 �̕�����y���̎���ɉ�]���邱�ƂɂȂ�܂��B��]���Ăł��鋅�̈ꕔ����
�̕�����y���̎���ɉ�]���邱�ƂɂȂ�܂��B��]���Ăł��鋅�̈ꕔ����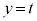 �Őؒf���Ăł���~�̔��a��2��́A�~C�̕�������
�Őؒf���Ăł���~�̔��a��2��́A�~C�̕�������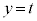 �Ƃ��āA
�Ƃ��āA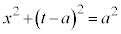 ���A
���A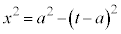 �C����āA�~C��
�C����āA�~C��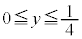 �̕�������]�����Ăł�����]�̂̑̐�
�̕�������]�����Ăł�����]�̂̑̐�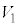 �́A
�́A 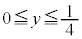 ����
����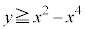 �ƂȂ镔���A�܂�
�ƂȂ镔���A�܂�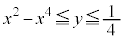 �ƂȂ镔����y���̎���ɉ�]�����Ăł����]�̂̑̐�
�ƂȂ镔����y���̎���ɉ�]�����Ăł����]�̂̑̐�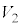 �́A�~�������ɂ��v�Z���܂��B�O�q�̂悤��
�́A�~�������ɂ��v�Z���܂��B�O�q�̂悤��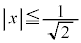 �ɂ�����
�ɂ�����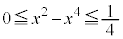 �Ȃ̂ŁA
�Ȃ̂ŁA(2)���A�̐�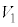 �̋��̈ꕔ���邢�͑S���͑̐�
�̋��̈ꕔ���邢�͑S���͑̐�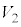 �̉�]�̂̓����ɂ���̂ŁA���߂�̐�
�̉�]�̂̓����ɂ���̂ŁA���߂�̐�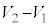 �́A
�́A 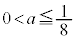 �̂Ƃ��A
�̂Ƃ��A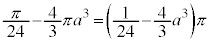 ......[��]
......[��]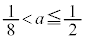 �̂Ƃ��A
�̂Ƃ��A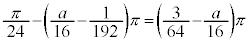 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B