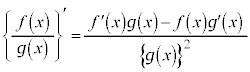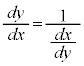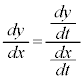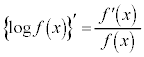微分法 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学Ⅲの微分では、三角関数、指数関数、対数関数の微分も扱います。微分計算の方法も、積の微分法、商の微分法、合成関数の微分法、など、多種の方法を学習します。またグラフを描くにあたり、1次導関数の正負による増減だけでなく、2次導関数による凹凸も調べます。
この項目では、平均変化率、微分・導関数、接線と微分係数、も参照してください。
ここで学習する内容は、以下の通りです。各項目をクリックしてください。
積の微分法 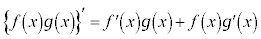
商の微分法 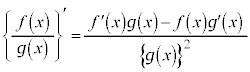
合成関数の微分法 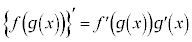 ,または、
,または、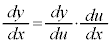
逆関数の微分法 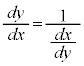
微分の公式 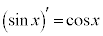 ,
,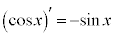 ,
,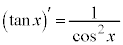 ,
,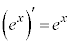 ,
,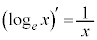
媒介変数表示された関数の微分法 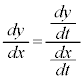
陰関数の微分法 円の方程式: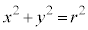 のようなものは、この形のまま合成関数の微分法を利用して微分し、
のようなものは、この形のまま合成関数の微分法を利用して微分し、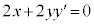 ,
,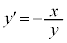 とします。
とします。
対数微分法 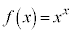 のようなそのままでは微分しにくい関数の場合、対数をとって微分するとうまくいくことがあります。
のようなそのままでは微分しにくい関数の場合、対数をとって微分するとうまくいくことがあります。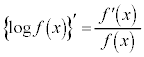
高次の導関数 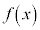 の導関数
の導関数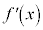 を1次の導関数と言います。
を1次の導関数と言います。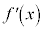 の導関数
の導関数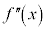 を2次の導関数と言います。
を2次の導関数と言います。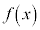 をn回微分した関数を
をn回微分した関数を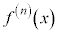 と書いて、n次の導関数と言います。
と書いて、n次の導関数と言います。
接線・法線の公式 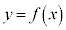 の点
の点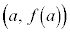 における接線:
における接線: ,法線(接点で接線と直交する直線):
,法線(接点で接線と直交する直線):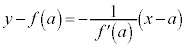
平均値の定理 閉区間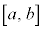 で連続、開区間
で連続、開区間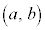 で微分可能な関数
で微分可能な関数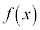 に対して、
に対して、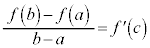 ,
,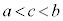 を満たすcが存在する。これを平均値の定理と言います。
を満たすcが存在する。これを平均値の定理と言います。
関数の増減 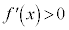 であれば、
であれば、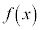 は増加、
は増加、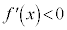 であれば、
であれば、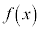 は減少。
は減少。
関数の凹凸 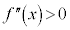 であれば、
であれば、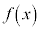 は下に凸、
は下に凸、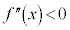 であれば、
であれば、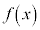 は上に凸。
は上に凸。
単調関数 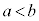 となるa,bについて、
となるa,bについて、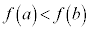 となる関数が単調増加関数、
となる関数が単調増加関数、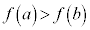 となる関数が単調減少関数。
となる関数が単調減少関数。
種々の関数のグラフ(1) 分数関数のグラフを考察します。
種々の関数のグラフ(2) 無理関数(根号を含む関数)のグラフを考察します。
種々の関数のグラフ(3) 三角関数を含む関数のグラフを考察します。
種々の関数のグラフ(4) 指数関数を含む関数のグラフを考察します。
種々の関数のグラフ(5) 対数関数を含む関数のグラフを考察します。
種々の関数のグラフ(6) 陰関数の形に表された関数のグラフを考察します。
種々の関数のグラフ(7) 媒介変数表示された関数のグラフを考察します。
関数の近似値 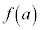 ,
,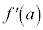 の値がわかっているとき、aに近いxについて、
の値がわかっているとき、aに近いxについて、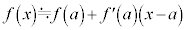 として、
として、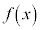 の近似値を求めることができます。
の近似値を求めることができます。
微分法の方程式への応用(2) 三角関数、指数関数を含む方程式の解の個数を調べる方法を学習します。
微分法の不等式への応用(2) 増減、凹凸を調べることにより、不等式を証明する方法を学習します。
マクローリン展開 関数値をより精密に近似する方法としてテーラー展開が知られています。マクローリン展開はテーラー展開の特別な場合です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。