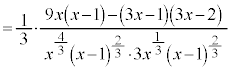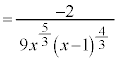��X�̊��̃O���t(2)�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�������̃O���t���l�@���܂��B���̍��ڂł́A�����̌����A���̑����A���̉������Q�Ƃ��Ă��������B
 ��1�D
��1�D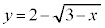
���̂��炢�Ȃ��������K�v�͂���܂���B��������0���A��`��́A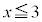
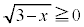 ���A�l��́A
���A�l��́A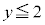
x��y�����ւ��āA
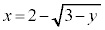
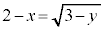
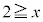 �Ƃ�����������2�悷��ƁA
�Ƃ�����������2�悷��ƁA
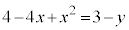
�� 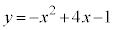
�Ƃ����킯�ŁA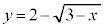 �̃O���t�́A�������F
�̃O���t�́A�������F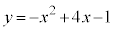 (2�������Q��)��
(2�������Q��)��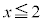 �̕�����
�̕�����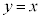 �Ɋւ��Đ܂�Ԃ����O���t�A�܂�A
�Ɋւ��Đ܂�Ԃ����O���t�A�܂�A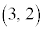 �_�Ƃ��鉡�ɐQ���������̎��̕Б��ɂȂ�܂��B
�_�Ƃ��鉡�ɐQ���������̎��̕Б��ɂȂ�܂��B
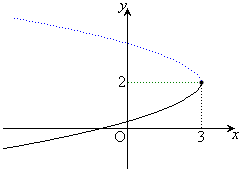
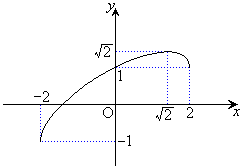
�������ł��邱�Ƃ��ӎ����A�K����x�ɐ��l������ē_���v���b�g���čs���悢�ł��傤�B�E�}�̂悤�ȃO���t�ɂȂ�܂��B
 ��2�D
��2�D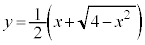
��������0���A��`��́A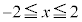
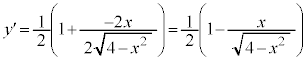 �@(�������̔����@���Q��)�@����@
�@(�������̔����@���Q��)�@����@
�@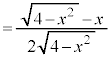
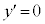 �Ƃ���ƁA
�Ƃ���ƁA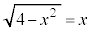
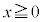 �Ƃ���2�悷��ƁA
�Ƃ���2�悷��ƁA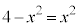
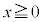 ���A
���A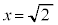
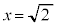 �̂Ƃ��A
�̂Ƃ��A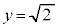 (�ő�l)
(�ő�l)
�@��������āA
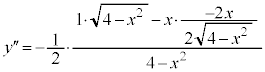 �@(���̔����@���Q��)
�@(���̔����@���Q��)
�@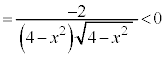 (�A���A
(�A���A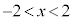 )
)
�]���āA�O���t��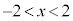 �͈̔͂ŏ�ɓʂȋȐ��ɂȂ�܂��B
�͈̔͂ŏ�ɓʂȋȐ��ɂȂ�܂��B
�����\�͈ȉ��̒ʂ�B�O���t�͉E�}(�ȉ~�ł�)�B
���D�@��������ƁA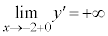 �C
�C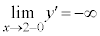 �ł��B�O���t�́A
�ł��B�O���t�́A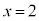 �ɂ�����x���ɐ����Ȑڐ�
�ɂ�����x���ɐ����Ȑڐ�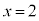 �C
�C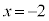 �ɂ�����x���ɐ����Ȑڐ�
�ɂ�����x���ɐ����Ȑڐ�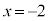 �������܂��B
�������܂��B
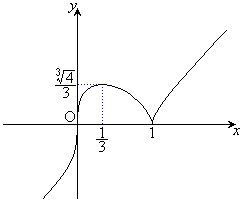 ��3�D
��3�D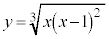
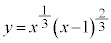
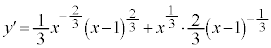 �@(�ς̔����@���Q��)
�@(�ς̔����@���Q��)
�@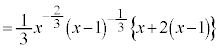
�@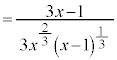
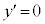 �Ƃ���ƁA
�Ƃ���ƁA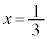
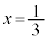 �̂Ƃ��A
�̂Ƃ��A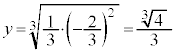 (�ɑ�l)
(�ɑ�l)
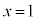 �̑O��ł�
�̑O��ł�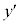 �̕������ω����邱�Ƃɒ��ӂ��Ă��������B
�̕������ω����邱�Ƃɒ��ӂ��Ă��������B �̂Ƃ��A
�̂Ƃ��A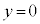 (�E�}�̂悤�ɁA
(�E�}�̂悤�ɁA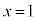 �̂Ƃ���ŃO���t���Ƃ���̂ł����A���������ꍇ�ł��A�ɏ��l�ƌ����܂��B���̂悤�ȓ_���_�ƌ����܂�)
�̂Ƃ���ŃO���t���Ƃ���̂ł����A���������ꍇ�ł��A�ɏ��l�ƌ����܂��B���̂悤�ȓ_���_�ƌ����܂�)
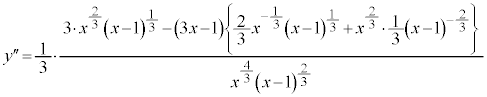 �@(���̔����@���Q��)
�@(���̔����@���Q��)
�@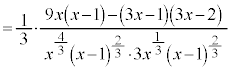
�@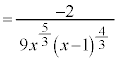
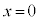 �̑O��ŁA
�̑O��ŁA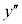 �̕������ω����邱�Ƃɒ��ӂ��Ă��������B
�̕������ω����邱�Ƃɒ��ӂ��Ă��������B
�����\�͈ȉ��̒ʂ�B�O���t�͉E�}�B
| x |
| 0 |
| 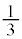 |
| 1 |
|
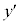 | �{ | �~ | �{ | 0 | �| | �~ | �| |
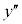 | �{ | �~ | �| | �| | �| | �~ | �| |
| y |  | 0 |  | 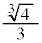 | 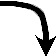 | 0 | 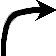 |
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �@(�������̔����@���Q��)�@����@
�@(�������̔����@���Q��)�@����@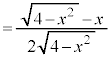
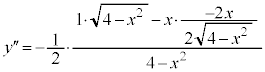 �@(���̔����@���Q��)
�@(���̔����@���Q��)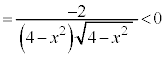 (�A���A
(�A���A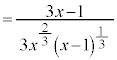
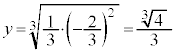 (�ɑ�l)
(�ɑ�l)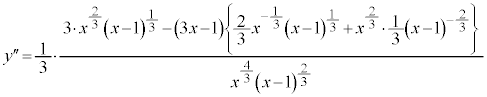 �@(���̔����@���Q��)
�@(���̔����@���Q��)