種々の関数のグラフ(3)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
この項目は、微分の公式、関数の増減、関数の凹凸を参照してください。
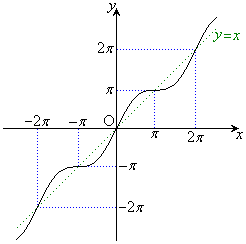 例1.
例1.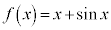
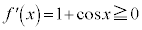 より、全実数xで単調増加です。
より、全実数xで単調増加です。
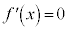 とすると、
とすると、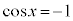 より、
より、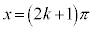 (kは奇数) となりますが、
(kは奇数) となりますが、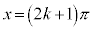 において、yは極値をとらないことに注意してください。
において、yは極値をとらないことに注意してください。
グラフは右図のようになります。
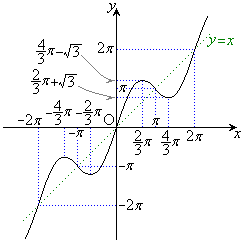 例2.
例2.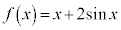
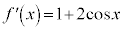
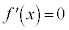 とすると、
とすると、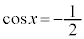 ,
,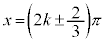 (kは整数)
(kは整数)
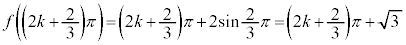 (極大値)
(極大値)
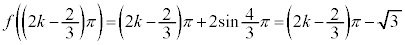 (極小値)
(極小値)
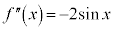
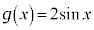 でも、
でも、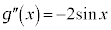 となるので、
となるので、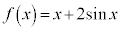 と
と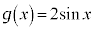 とで凹凸は同じです。
とで凹凸は同じです。
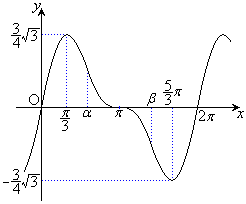
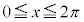 における増減表は以下の通りです。グラフは右図。
における増減表は以下の通りです。グラフは右図。
 例3.
例3.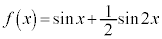
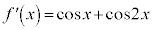
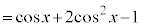 (2倍角の公式を参照)
(2倍角の公式を参照)
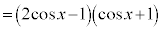
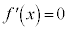 とすると、
とすると、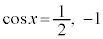
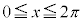 においては、
においては、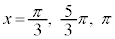 (
(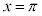 において、yは極大でも極小でもありません)
において、yは極大でも極小でもありません)
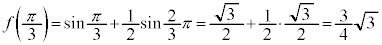 (極大値)
(極大値)
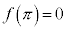
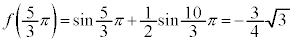 (極小値)
(極小値)
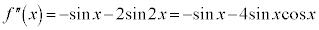 (2倍角の公式を参照)
(2倍角の公式を参照)
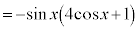
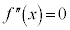 とすると、
とすると、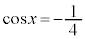 ,これを満たすxは、
,これを満たすxは、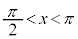 ,
,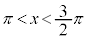 の範囲に各1個あります。これを、α,βとします。
の範囲に各1個あります。これを、α,βとします。
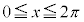 における増減表(周期
における増減表(周期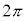 の周期関数なので、
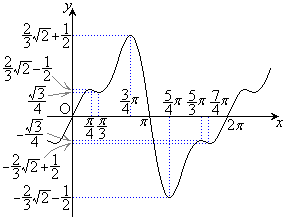
の周期関数なので、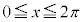 以外の部分においても同じことが繰り返されるだけです)は以下の通りです。グラフは右図。
以外の部分においても同じことが繰り返されるだけです)は以下の通りです。グラフは右図。
| x | 0 |
| 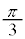 |
| α |
| π |
| β |
| 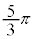 |
| 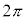 |
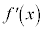 | + | + | 0 | − | − | − | 0 | − | − | − | 0 | + | + |
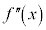 | − | − | − | − | 0 | + | 0 | − | 0 | + | + | + | 0 |
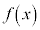 | 0 |  | 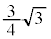 |  |
|  | 0 |  |
|  | 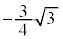 |  | 0 |
 例4.
例4.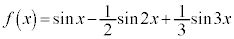
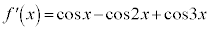
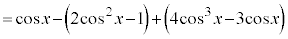 (2倍角の公式、三角関数の諸公式を参照)
(2倍角の公式、三角関数の諸公式を参照)
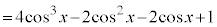
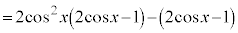
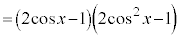
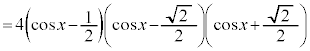
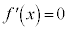 とすると、
とすると、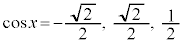
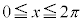 においては、
においては、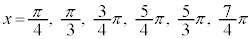
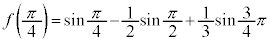
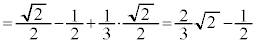 (極大値)
(極大値)
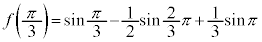
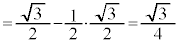 (極小値)
(極小値)
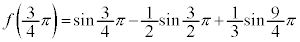
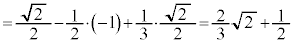 (極大値)
(極大値)
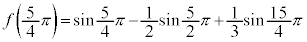
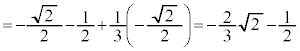 (極小値)
(極小値)
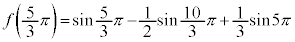
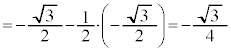 (極大値)
(極大値)
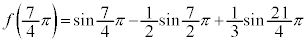
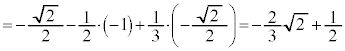 (極小値)
(極小値)
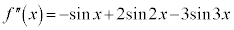
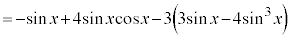
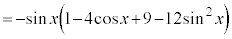
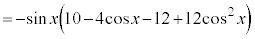
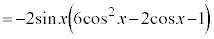
これより、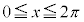 においては、
においては、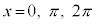 において変曲点になることがわかりますが、その他の変曲点(4個あります)のx座標をきれいな形に求めることはできません。
において変曲点になることがわかりますが、その他の変曲点(4個あります)のx座標をきれいな形に求めることはできません。
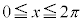 における増減表(周期
における増減表(周期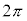 の周期関数なので、
の周期関数なので、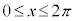 以外の部分においても同じことが繰り返されるだけです)は以下の通りです。グラフは右図。
以外の部分においても同じことが繰り返されるだけです)は以下の通りです。グラフは右図。
注.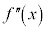 を入れると増減表が複雑になるので、
を入れると増減表が複雑になるので、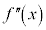 を省略しました。
を省略しました。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 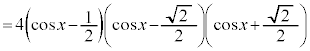
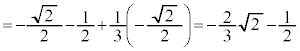 (極小値)
(極小値)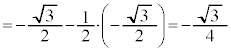 (極大値)
(極大値)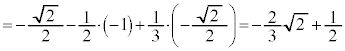 (極小値)
(極小値)