種々の関数のグラフ(5)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
この項目は、微分の公式、関数の増減、関数の凹凸を参照してください。
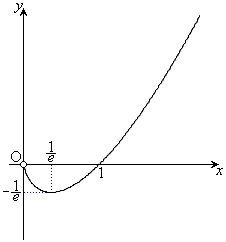 例1.
例1.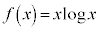
定義域は、真数条件(対数関数を参照)より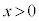
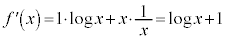 (積の微分法を参照)
(積の微分法を参照)
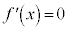 とすると、
とすると、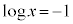
∴ 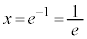
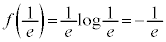 (極小値)
(極小値)
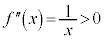 (
(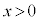 )
)
従って、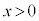 において、グラフは下に凸。
において、グラフは下に凸。
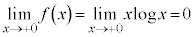 (
(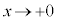 のとき、
のとき、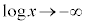 ですが、xの方が収束する勢いが強い),
ですが、xの方が収束する勢いが強い),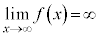
増減表は以下の通り。グラフは右図。
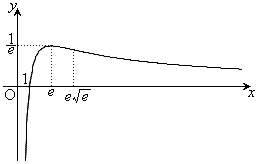 例2.
例2.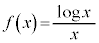
定義域は、真数条件より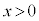
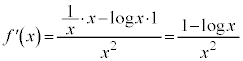 (商の微分法を参照)
(商の微分法を参照)
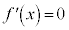 とすると、
とすると、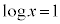
∴ 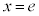
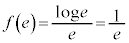 (極大値)
(極大値)
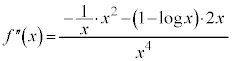
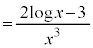
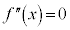 とすると、
とすると、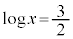
∴ 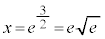
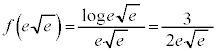
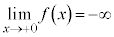 ,
,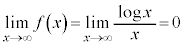 (
(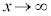 のとき、
のとき、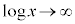 ですが、xの方が収束する勢いが強い)
ですが、xの方が収束する勢いが強い)
増減表は以下の通り。グラフは右図。
グラフは、変曲点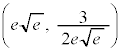 をもちます。
をもちます。
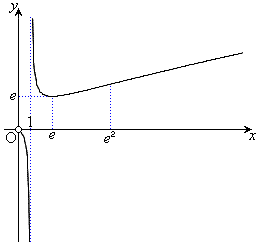 例3.
例3.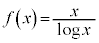
定義域は、真数条件より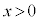 ,また、
,また、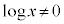 より
より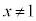 ,よって、定義域は、
,よって、定義域は、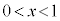 ,
,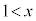
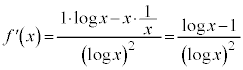 (商の微分法を参照)
(商の微分法を参照)
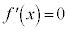 とすると、
とすると、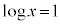
∴ 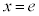
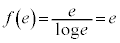 (極小値)
(極小値)
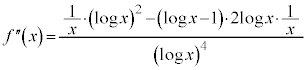
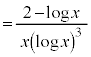
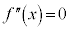 とすると、
とすると、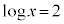
∴ 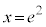
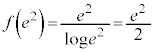
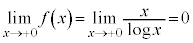 (
(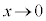 のとき、
のとき、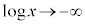 ですが、xの方が収束する勢いが強い)
ですが、xの方が収束する勢いが強い)
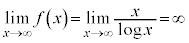 (
(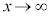 のとき、
のとき、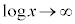 ですが、xの方が収束する勢いが強い)
ですが、xの方が収束する勢いが強い)
増減表は以下の通り。グラフは右図。
グラフは、変曲点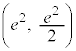 をもちます。
をもちます。
 例4.
例4.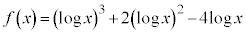
定義域は、真数条件より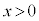
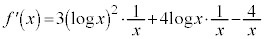
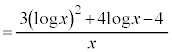
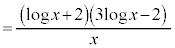
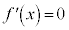 とすると、
とすると、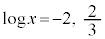
∴ 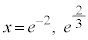
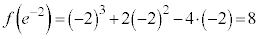 (極大値)
(極大値)
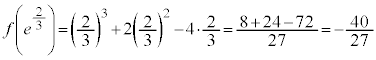 (極小値)
(極小値)
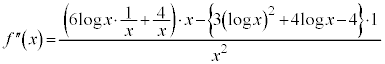
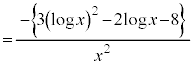
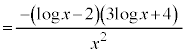
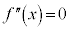 とすると、
とすると、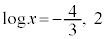
∴ 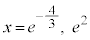
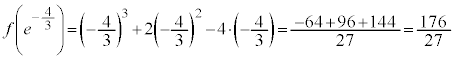
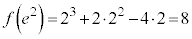
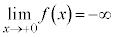 ,
,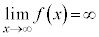
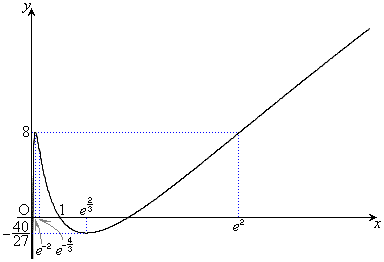
増減表は以下の通り。グラフは右図。
| x | 0 |
| 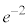 |
| 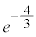 |
| 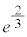 |
| 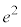 |
|
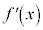 | × | + | 0 | − | − | − | 0 | + | + | + |
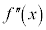 | × | − | − | − | 0 | + | + | + | 0 | − |
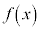 | × | 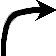 | 8 |  | 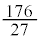 |  | 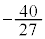 |  | 8 |  |
グラフは、変曲点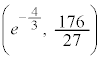 ,
,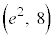 をもちます。
をもちます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 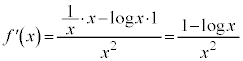 (商の微分法を参照)
(商の微分法を参照)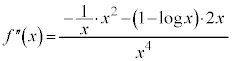
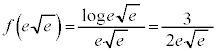
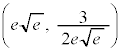 をもちます。
をもちます。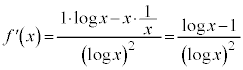 (商の微分法を参照)
(商の微分法を参照)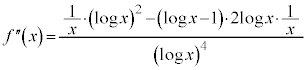
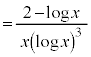
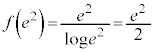
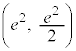 をもちます。
をもちます。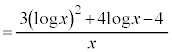
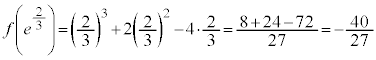 (極小値)
(極小値)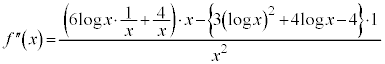
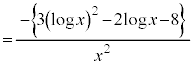
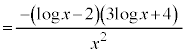
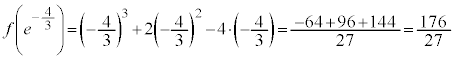
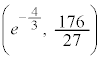 ,
,