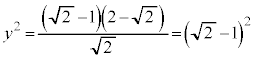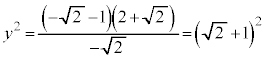��X�̊��̃O���t(6)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���̍��ڂ́A�����̌����A���̑����A���̉������Q�Ƃ��Ă��������B
 ��1�D
��1�D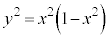
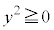 �C
�C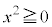 ���A
���A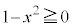
����āA���̒�`��́A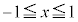
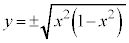 �Ə������Ƃ��ł��܂����A����́A�O���t��x���Ɋւ��đΏ̂ɂȂ邱�Ƃ��Ӗ����Ă��܂��B
�Ə������Ƃ��ł��܂����A����́A�O���t��x���Ɋւ��đΏ̂ɂȂ邱�Ƃ��Ӗ����Ă��܂��B
�A���̔����@�ɂ���������ƁA
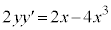
�� 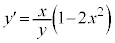 �@����@
�@����@
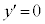 �Ƃ���ƁA
�Ƃ���ƁA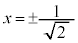 �@(
�@(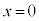 �̂Ƃ�
�̂Ƃ�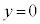 ���
���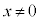 �C�ł����@�́A
�C�ł����@�́A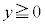 �ɂ��ẮA
�ɂ��ẮA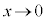 �̂Ƃ��A
�̂Ƃ��A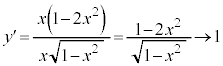 )
)
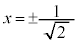 �̂Ƃ��A
�̂Ƃ��A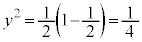
�� 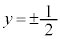
�@�����̔����@�ɂ���������ƁA
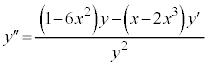
�@�������āA
�@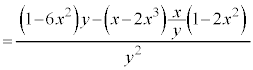
�@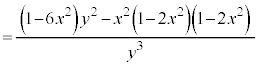
�@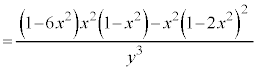
�@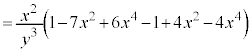
�@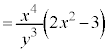
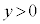 �Ȃ�A��`��
�Ȃ�A��`��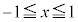 �ɂ����ẮA
�ɂ����ẮA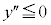
�]���āA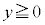 �ɂ����ẮA�O���t�͏�ɓʁB
�ɂ����ẮA�O���t�͏�ɓʁB
�O���t��x���Ɋւ��đΏ̂Ȃ̂ŁA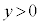 �̕������l�����Ƃ��̑����\�͈ȉ��̒ʂ�B
�̕������l�����Ƃ��̑����\�͈ȉ��̒ʂ�B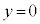 (x����)�̂Ƃ�
(x����)�̂Ƃ�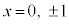 �C
�C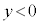 �̕����ɂ��ẮA
�̕����ɂ��ẮA �̕�����x���Ɋւ��đΏ̂ɐ܂�Ԃ��āA�O���t�͉E�}�B
�̕�����x���Ɋւ��đΏ̂ɐ܂�Ԃ��āA�O���t�͉E�}�B
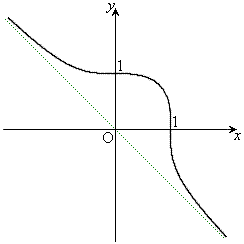 ��2�D
��2�D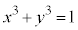
�A���̔����@�ɂ���������ƁA
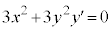
�� 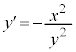 (
(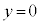 �̂Ƃ�
�̂Ƃ�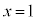 ���A
���A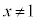 )
)
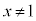 �ɂ�����
�ɂ�����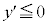 ���Ay�͒P�������ŃO���t�͉E������ł��B
���Ay�͒P�������ŃO���t�͉E������ł��B
���̔����@�ɂ���������ƁA
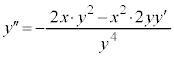
�@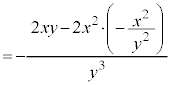
�@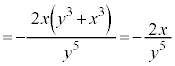
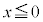 �̂Ƃ��A
�̂Ƃ��A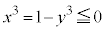 ���A
���A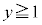
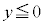 �̂Ƃ��A
�̂Ƃ��A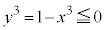 ���A
���A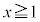
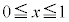 �̂Ƃ��A
�̂Ƃ��A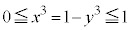 ���A
���A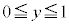
�ȏ���A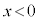 �̂Ƃ��A
�̂Ƃ��A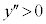 �ŁA�O���t�͉��ɓʁB
�ŁA�O���t�͉��ɓʁB
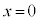 �̂Ƃ��A
�̂Ƃ��A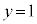 �C
�C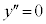 �ŁA
�ŁA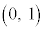 ���ϋȓ_�B
���ϋȓ_�B
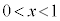 �̂Ƃ��A
�̂Ƃ��A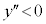 �ŁA�O���t�͏�ɓʁB
�ŁA�O���t�͏�ɓʁB
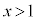 �̂Ƃ��A
�̂Ƃ��A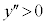 �ŁA�O���t�͉��ɓʁB
�ŁA�O���t�͉��ɓʁB
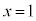 �̂Ƃ��A
�̂Ƃ��A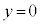 �ŁA
�ŁA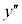 �͒�`�ł��Ȃ����A
�͒�`�ł��Ȃ����A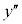 �̕����������ŕω�����̂ŁA
�̕����������ŕω�����̂ŁA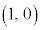 �͕ϋȓ_�B
�͕ϋȓ_�B
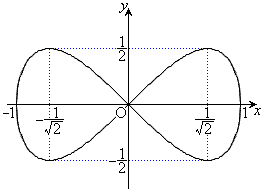
�ȏ���A�O���t�͉E�}�B
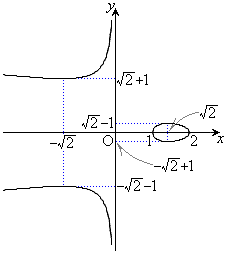 ��3�D
��3�D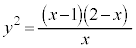
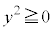 ���A
���A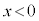 �C
�C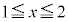
����āA���̒�`��́A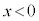 �C
�C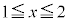
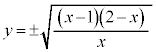 �Ə������Ƃ��ł��܂����A����́A�O���t��x���Ɋւ��đΏ̂ɂȂ邱�Ƃ��Ӗ����Ă��܂��B
�Ə������Ƃ��ł��܂����A����́A�O���t��x���Ɋւ��đΏ̂ɂȂ邱�Ƃ��Ӗ����Ă��܂��B
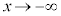 �̂Ƃ��A
�̂Ƃ��A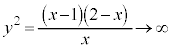 ���A
���A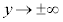
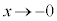 �̂Ƃ��A
�̂Ƃ��A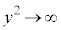 ���A
���A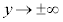
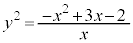
�A���̔����@�A���̔����@�ɂ���������ƁA
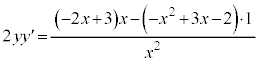
�@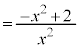
�� 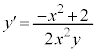 �@����@
�@����@
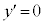 �Ƃ���ƁA
�Ƃ���ƁA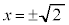
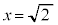 �̂Ƃ��A
�̂Ƃ��A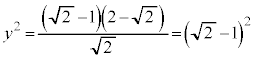
�� 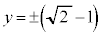
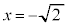 �̂Ƃ��A
�̂Ƃ��A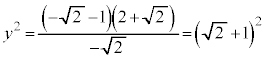
�� 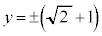
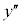 �͕��G�ɂȂ�̂ŏȗ����܂��B
�͕��G�ɂȂ�̂ŏȗ����܂��B
�O���t��x���Ɋւ��đΏ̂Ȃ̂ŁA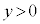 �̕������l�����Ƃ��̑����\�͈ȉ��̒ʂ�B
�̕������l�����Ƃ��̑����\�͈ȉ��̒ʂ�B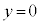 �̂Ƃ�(x����)��
�̂Ƃ�(x����)��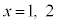 �C
�C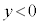 �̕����ɂ��ẮA
�̕����ɂ��ẮA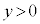 �̕�����x���Ɋւ��đΏ̂ɐ܂�Ԃ��āA�O���t�͉E�}�B
�̕�����x���Ɋւ��đΏ̂ɐ܂�Ԃ��āA�O���t�͉E�}�B
| x |
| 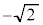 |
| 0 |
| 1 |
| 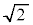 |
| 2 |
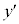 | �| | 0 | �{ | �~ | �~ | �~ | �{ | 0 | �| | �~ |
| y |  | 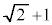 |  | �~ | �~ | 0 |  | 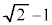 |  | 0 |
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 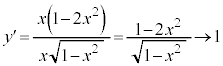 )
)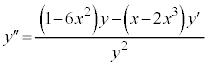
 (
(
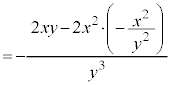
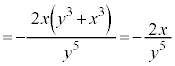
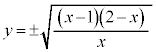 �Ə������Ƃ��ł��܂����A����́A�O���t��x���Ɋւ��đΏ̂ɂȂ邱�Ƃ��Ӗ����Ă��܂��B
�Ə������Ƃ��ł��܂����A����́A�O���t��x���Ɋւ��đΏ̂ɂȂ邱�Ƃ��Ӗ����Ă��܂��B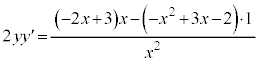
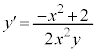 �@����@
�@����@