円と放物線の位置関係 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
例1.原点でx軸と接する 円 :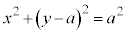 (
(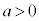 )と放物線:
)と放物線: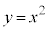 の位置関係を考察します。
の位置関係を考察します。
放物線: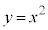 上の点
上の点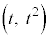 と円の中心
と円の中心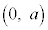 との距離dの2乗は、
との距離dの2乗は、
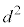 と円の半径の2乗
と円の半径の2乗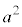 との大小関係を考えればよいのですが、
との大小関係を考えればよいのですが、
の正負を考えることになります。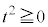 ですが、
ですが、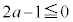 ,つまり、
,つまり、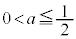 のとき、全実数tについて、
のとき、全実数tについて、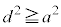 (等号は
(等号は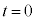 のとき、
のとき、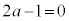 )です。このとき、円と放物線は原点で接します。それ以外は
)です。このとき、円と放物線は原点で接します。それ以外は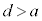 で、放物線上の点は円の外部にあります(不等式の表す領域を参照)。
で、放物線上の点は円の外部にあります(不等式の表す領域を参照)。
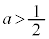 ,つまり、
,つまり、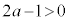 のとき、
のとき、
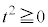 ですが、
ですが、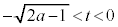 ,
,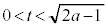 のとき、
のとき、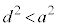 ,このとき、放物線上の点は円の内部にあります。
,このとき、放物線上の点は円の内部にあります。
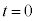 のとき、
のとき、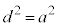 ,このとき、円と放物線は原点で接します。
,このとき、円と放物線は原点で接します。
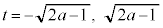 ,つまり、
,つまり、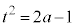 のとき、放物線は円と交わります。
のとき、放物線は円と交わります。
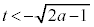 ,
,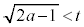 ,つまり、
,つまり、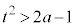 のとき、
のとき、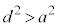 ,このとき、放物線上の点は円の外部にあります。
,このとき、放物線上の点は円の外部にあります。
以上まとめると、
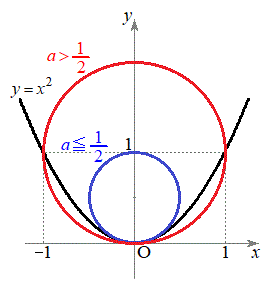 (i)
(i)  のとき、円と放物線は原点で接し、それ以外は放物線上の点は円の外部にあります。
のとき、円と放物線は原点で接し、それ以外は放物線上の点は円の外部にあります。(ii) 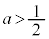 のとき、円と放物線は原点で接し、
のとき、円と放物線は原点で接し、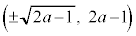 において、交わり、
において、交わり、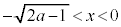 ,
,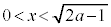 においては放物線上の点は円の内部にあり、
においては放物線上の点は円の内部にあり、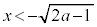 ,
,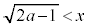 においては、放物線上の点は円の外部にあります。
においては、放物線上の点は円の外部にあります。
例2.放物線: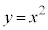 と、放物線の軸上に中心をもつ 円 :
と、放物線の軸上に中心をもつ 円 :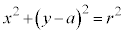 (
(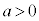 ,
,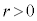 )の位置関係を考察します。
)の位置関係を考察します。
放物線: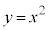 上の点
上の点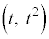 と円の中心
と円の中心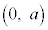 との距離dの2乗は、
との距離dの2乗は、
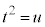 (
(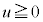 )とおくと、
)とおくと、
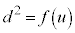 としてuの2次関数と見ると、グラフは
としてuの2次関数と見ると、グラフは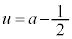 を軸とする放物線です。軸の位置によって場合分けします。
を軸とする放物線です。軸の位置によって場合分けします。
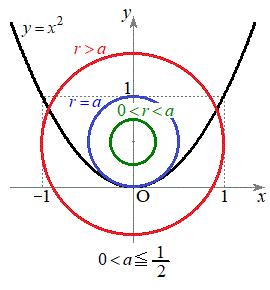 (i)
(i) 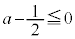 ,即ち
,即ち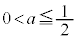 のとき、
のとき、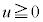 において
において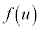 は単調増加で、
は単調増加で、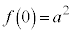 より、2次方程式
より、2次方程式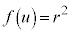 は、
は、・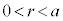 のとき、解はなく、円と放物線に共有点はありません。
のとき、解はなく、円と放物線に共有点はありません。 ・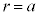 のとき、
のとき、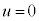 という解をもち、このとき、
という解をもち、このとき、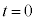 で、円と放物線は、原点で接します。他に共有点はありません。
で、円と放物線は、原点で接します。他に共有点はありません。 ・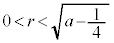 のとき、解はなく、円と放物線に共有点はありません。
のとき、解はなく、円と放物線に共有点はありません。 ・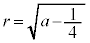 のとき、
のとき、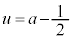 という解をもち、このとき、
という解をもち、このとき、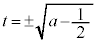 において、円と放物線が接します。他に共有点はありません。
において、円と放物線が接します。他に共有点はありません。 ・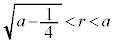 のとき、
のとき、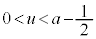 の範囲に解
の範囲に解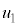 ,
,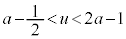 の範囲に解
の範囲に解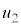 をもち、このとき、
をもち、このとき、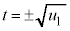 ,
,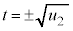 において、円と放物線は交わります。他に共有点はありません。
において、円と放物線は交わります。他に共有点はありません。 ・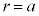 のとき、例1の(ii)より、円と放物線は原点で接し、
のとき、例1の(ii)より、円と放物線は原点で接し、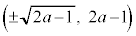 において交わります。
において交わります。 ・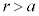 のとき、
のとき、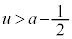 の範囲に解
の範囲に解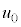 をもち、
をもち、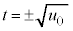 において、円と放物線が交わります。他に共有点はありません。
において、円と放物線が交わります。他に共有点はありません。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。