東大理系数学'04年前期[2]
自然数の2乗になる数を平方数という。以下の問いに答えよ。
(1) 10進法で表して3桁以上の平方数に対し、10の位の数をa,1の位の数をbとおいたとき、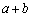 が偶数となるならば、bは0または4であることを示せ。
が偶数となるならば、bは0または4であることを示せ。 (2) 10進法で表して5桁以上の平方数に対し、1000の位の数、100の位の数、10の位の数、および1の位の数の4つすべてが同じ数となるならば、その平方数は10000で割り切れることを示せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (1)は、結局、もとの数の1の位の数字で決まります。(2)は(1)が利用できそうです。なお、整数を参照して下さい。
(1) pを自然数、qを0から9の間の整数とします。3桁以上の平方数Nは10以上の整数の2乗なので、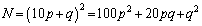 と表せます。
と表せます。 Nの10の位の数字aは、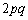 +(
+(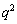 の10の位の数字) の1の位の数字になります。Nの1の位の数字bは
の10の位の数字) の1の位の数字になります。Nの1の位の数字bは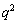 の1の位の数字になります。
の1の位の数字になります。
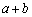 はの偶奇は、
はの偶奇は、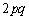 +(
+(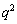 の10の位の数字)+(
の10の位の数字)+(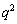 の1の位の数字) の偶奇と一致します。
の1の位の数字) の偶奇と一致します。
このうち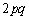 は偶数だから、
は偶数だから、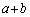 の偶奇は、(
の偶奇は、(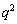 の10の位の数字)+(
の10の位の数字)+(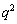 の1位の数字) の偶奇と一致します。
の1位の数字) の偶奇と一致します。
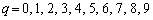 に対して、(
に対して、(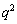 の10の位の数字)+(
の10の位の数字)+(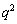 の1位の数字) は、
の1位の数字) は、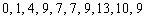 となります。
となります。
よって、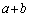 が偶数となるのは、
が偶数となるのは、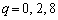 のときです。bは
のときです。bは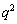 の1の位の数字なので、
の1の位の数字なので、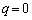 のとき
のとき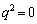 で
で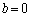 ,
,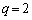 のとき
のとき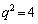 で
で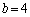 ,
,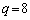 のとき
のとき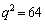 で
で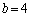 となります。
となります。
よって、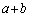 が偶数ならば、bは0または4です。
が偶数ならば、bは0または4です。
(2) 題意を満たす平方数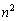 (nは自然数)の、10の位の数と1の位の数が等しいので、両者の和は偶数です。すると(1)が利用できます。
(nは自然数)の、10の位の数と1の位の数が等しいので、両者の和は偶数です。すると(1)が利用できます。 (1)より、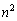 の1の位は0または4です。
の1の位は0または4です。
・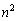 の1の位の数字が0のとき、
の1の位の数字が0のとき、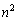 の下4桁は0000だから、
の下4桁は0000だから、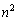 は10000で割り切れます。
は10000で割り切れます。
・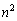 の1の位の数字が4のとき、
の1の位の数字が4のとき、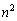 は下4桁は4444で偶数です。このとき、nも偶数であって、
は下4桁は4444で偶数です。このとき、nも偶数であって、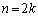 (kは自然数)とおけます。
(kは自然数)とおけます。 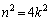 の下4桁が4444ですから、mを自然数として、
の下4桁が4444ですから、mを自然数として、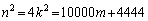 とおくと、
とおくと、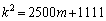 であって、
であって、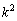 の10の位の数と1の位の数の和、
の10の位の数と1の位の数の和、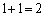 は偶数になります。すると、(1)より、
は偶数になります。すると、(1)より、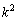 の1の位の数は0か4のはずですが、
の1の位の数は0か4のはずですが、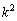 の1の位の数字は1であって0でも4でもないので(1)と矛盾してしまいます。よって、
の1の位の数字は1であって0でも4でもないので(1)と矛盾してしまいます。よって、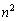 の1位の数字は4になり得ないのです。
の1位の数字は4になり得ないのです。
以上より、5桁以上の平方数の下4桁がすべて同じ数ならその平方数は10000で割り切れます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。