東大理系数学'04年前期[4]
関数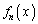
(
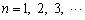)を次のように定める。
以下同様に、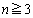
に対して関数
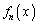が定まったならば、関数
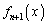を
で定める。このとき、以下の問いに答えよ。
(1) aを実数とする。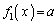
を満たす実数xの個数を求めよ。 (2) aを実数とする。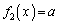
を満たす実数xの個数を求めよ。 (3) nを3以上の自然数とする。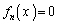
を満たす実数xの個数は
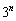であることを示せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答(3)は、数学的帰納法ということははっきりしていますが、少々、工夫が必要です。
，
，
，
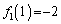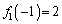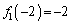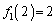より、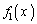
の増減表は以下の通り(3次関数の増減を参照)。
また、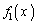
のグラフは右図の通り。グラフより、
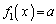を満たす実数xの個数は、・
，
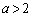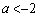のとき、1個 ・
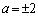のとき、2個 ・
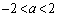のとき、3個 ......[答] (2) 
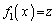とおく。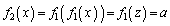
を満たすzの個数は(1)で調べています。
・
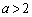のとき、(1)のグラフより、
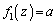を満たすzは、
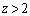の範囲に1個だけあります。 (1)より、このzに対して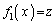
を満たす実数xの個数は1個 ......[答]
・
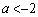のとき、(1)のグラフより、
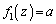を満たすzは、
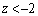の範囲に1個だけあります。 (1)より、このzに対して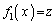
を満たす実数xの個数は1個 ......[答]
(1)より、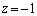
のとき
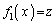を満たす実数xは3個、
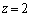のとき、
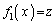を満たす実数xは
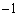と2の2個。
合わせて、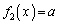
を満たす実数xの個数は5個 ......[答]
(1)より、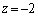
のとき、
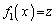を満たす実数xは
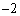と1の2個、
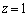のとき、
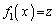を満たす実数xは3個。
合わせて、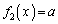
を満たす実数xは5個 ......[答]
・
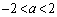のとき、(1)のグラフより、
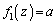を満たすzは、
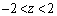の範囲に3個あり、各々の値を、
，
，
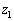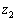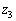とします。 
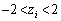より、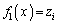
(
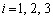)を満たす実数xは
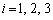の各々について3個ずつ計9個とれます。
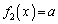を満たす実数xは9個 ......[答]
(3) 「自然数」に関する証明問題なので、数学的帰納法で証明するのがラクそうです。
問題文では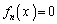
となっているのですが、
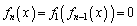のとき、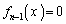
というわけではありません。
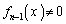であっても、
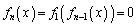となる可能性があります。
従って、問題文のままでは数学的帰納法に乗せにくいのです。(2)の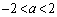
のときにxが9 (
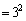)個とれたということは、
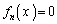に限らずに、
(
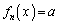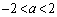)としてもやはりxは
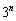個とれるだろう、と思われます。というわけで、数学的帰納法で、
「aが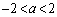
を満たす実数だとして、
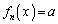を満たす実数xの個数は
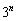個ある」 ･･･(＊)という命題を証明することにします。この証明ができてから
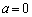とすればよいでしょう。
また、問題文では、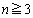
について示せとなっているのですが、
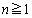として示しておけば、
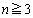でも成り立つので、ここでは、
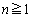として数学的帰納法の証明をすることにします。
・
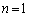のとき、(1)より、aが
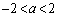を満たす実数だとして、
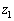を満たす実数xは、
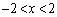の範囲に
個あるから、命題(＊)は成り立ちます。 ・
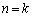のとき命題(＊)が成り立つと仮定します。つまり、aが
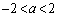を満たす実数だとして、
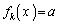を満たす実数xの個数が
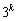個あるとします。 今度は、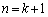
のとき、aが
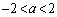を満たす実数だとして、
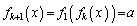を満たす実数xの個数を考えます。
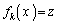とおくと、
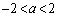より、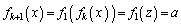
を満たす実数zは、(1)より、
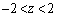の範囲に3個あり、各々の値を、
，
，
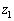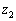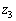とします。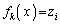
(
)(
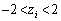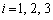)を満たす実数xは
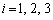の各々について
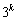個ずつ、計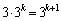
個あります。
よって、aが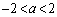
を満たす実数だとして、
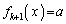を満たす実数xの個数は
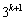個あり、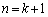
のときも命題は成立します。 以上より、数学的帰納法により命題(＊)を証明することができます。
この命題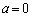で
として、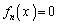
を満たす実数xの個数は、
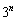個 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
(1) 
，
のとき、
の3解はいずれも、グラフより、
の範囲に存在します。
のとき、(1)のグラフより、
を満たすzは、
のとき、(1)のグラフより、
を満たすzは、
