東大理系数学'05年前期[4]
3以上9999以下の奇数aで、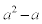
が10000で割り切れるものをすべて求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 東大では頻出の整数問題です。整数を参照してください。
まず、kを自然数だとして、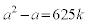
とおいてみます。
これをaの2次方程式とみて解くと、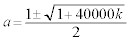
ここで根号が開ける、つまり、根号内が平方数である条件を考えればよいのですが、
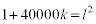などと置いてもちょっと展望はないですね。
9999は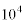
に近いのですが、
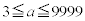のとき、
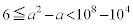となりますが、
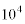で割っても、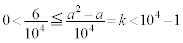
これでは、kとして調べる範囲が広すぎます。
よって、この方針はボツ。
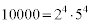なので、
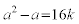とか、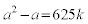
とかして、2次方程式を解く方針も考えられますが、先の方針と似たり寄ったりでしょうね。
次に、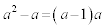
と因数分解してみます。
これで、1つ気がつかないといけないことがあります。
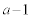，aは連続している2整数です。片方が奇数で、もう一方は偶数です。また、aと
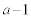は、互いに素(2以上の約数を持たない)です。
とるに足らないような当たり前のことですが、こういうことが整数の問題では非常に役立つときがあります。
10000を素因数分解して出てくる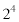
は偶数です。
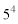は奇数です。
ということは、次の2つの場合しかあり得ないということです。
これ以外の場合(たとえば、片方が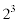
の倍数で、他方が
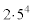の倍数になるような場合には、2数がともに偶数になってしまいます)はあり得ません。
(i)の場合、kを整数として、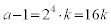
とおくと、lを整数として、 
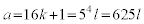とおけます。つまり、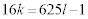
この左辺は偶数なので、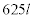
は奇数です。lも奇数です。
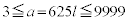より、
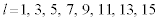の8通りに限られます。
この程度なら全数チェックしてもよいでしょう。
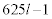と書ける数の中から16の倍数になるものを探します。
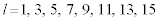の各々について、
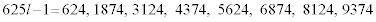となりますが、
このうち、16の倍数は、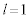
に対応する624だけです。
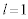のとき、
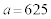です。
原問題のままなら、aが奇数になるのは(i)の場合だけなので、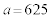
......[答]
ここでは、aが偶数の場合も調べておきます。
(ii)の場合、kを整数として、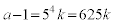
とおくと、lを整数として、 
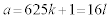とおけます。
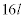は偶数なので、
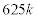は奇数となり、kも奇数です。
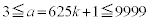より、
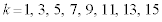の8通りに限られます。
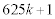と書ける数の中から16の倍数になるものを探します。
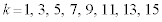の各々について、
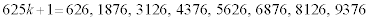
このうち、16の倍数は、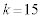
に対する9376だけです。
よって、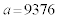
この問題では、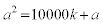
，つまり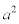
の下4桁がaに一致していると言っているわけですが、実際、
，
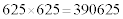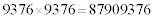となります。
小学生の家庭教師のアルバイトをやっていて、かけ算の練習をさせるとき、
何でもよいから、3桁の数を考えてごらん、と言って、
小学生が、例えば、293を考えたとします。
まず、7をかけてみてね、と、言います。
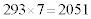となります。
次に、今出てきた答に11をかけてみてね、と、言います。
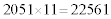となります。
さらに、今出てきた答に13をかけてみてね、と、言います。
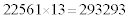となります。
はじめに考えた数と比べてごらん、と言うと、小学生が計算間違いをしていなければ、
目を丸くします。
なぜだろうね？と言って理由を考えさせるのもよいかもしれません。
ほかにも3桁の数を考えさせて、計算を何回かやらせるうちに、7と11と13にトリックがあるな、ということに気づかせることができるでしょう。
要するに、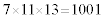
だからなのですが、こんなことからでも、小学生に数の不思議さを体験させて科学への興味を持たせることができれば素敵だと思いませんか？
原問題がaを奇数の場合に限っているのは、(i)も(ii)も結局同じことを2度やるだけなので、無駄かなと出題者が思ったからだと思いますが、(ii)の手間を省略したければ、
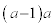がmの倍数であって、nを整数として、
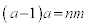と書けるとき、
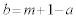とすると、
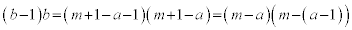
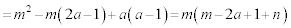より、
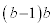もmの倍数です。この問題でaが偶数でよいことにすると、
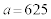が答なら、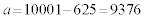
も答です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
が
の倍数でaが
の倍数
が
の倍数でaが
の倍数