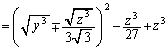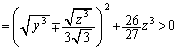東大文系数学'06年前期[3]
nを正の整数とする。実数x,y,zに対する方程式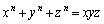 ・・・① を考える。
・・・① を考える。
(1) 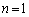 のとき、①を満たす正の整数の組
のとき、①を満たす正の整数の組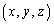 で
で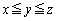 となるものをすべて求めよ。
となるものをすべて求めよ。 (2) 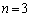 のとき、①を満たす正の実数の組
のとき、①を満たす正の実数の組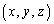 は存在しないことを示せ。
は存在しないことを示せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 整数問題で、すべての場合をチェックするとしたら無限の可能性があって、チェックしきれません。そこで、チェックする範囲を与えられた条件を使って絞り込む(できれば、10通り以内くらいに)必要があります。(1)では、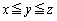 という条件をうまく使うことがカギです。
という条件をうまく使うことがカギです。
(2)は整数問題ではありませんが、いろいろな解法が考えられます。
(1) ①で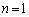 とすると、
とすると、 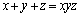 ・・・②
・・・②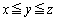 より、
より、②より、
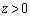 より、
より、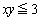 x,yは正の整数なので、
x,yは正の整数なので、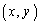 =
=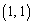 ,
,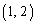 ,
,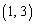 ,
,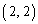 ,
,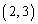 ,
,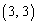 に限られます。
に限られます。・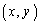 =
=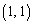 のとき、
のとき、 ②より、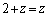 となり不適。
となり不適。 ・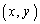 =
=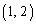 のとき、
のとき、 ②より、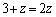 ,
,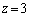
・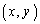 =
=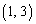 のとき、
のとき、 ・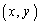 =
=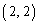 のとき、
のとき、 ②より、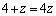 ,
,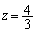 となり不適。
となり不適。 ・ =
= のとき、
のとき、 ・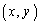 =
=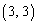 のとき、
のとき、 ②より、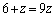 ,
,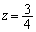 となり不適。
となり不適。 以上より、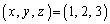 ......[答]
......[答]
(2) ①で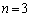 とすると、
とすると、 これを満たす正の実数の組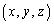 が存在すると仮定します。
が存在すると仮定します。
これをxに関する3次方程式と見て、 増減表より、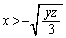 において
において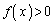 であって、3次方程式
であって、3次方程式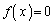 は、正の実数解をもちません。これは、
は、正の実数解をもちません。これは、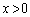 という仮定と矛盾します。よって、正の実数の組
という仮定と矛盾します。よって、正の実数の組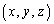 が存在するとした仮定は誤りであって、
が存在するとした仮定は誤りであって、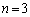 のとき、①を満たす正の実数の組
のとき、①を満たす正の実数の組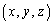 は存在しません。別解 相加平均相乗平均の関係より、
は存在しません。別解 相加平均相乗平均の関係より、 よって、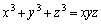 をみたす正の実数の組
をみたす正の実数の組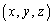 は存在しません。
は存在しません。
追記.(1)は、東工大'96年前期[1](以下)の一部分((1)の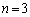 の場合)です。
の場合)です。
2以上の整数nに対して方程式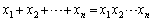 の正の整数解
の正の整数解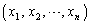 を考える。ただし、たとえば
を考える。ただし、たとえば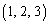 と
と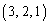 は異なる解とみなす。このとき次の問いに答えよ。
は異なる解とみなす。このとき次の問いに答えよ。 (1) 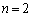 および
および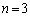 のときの解をすべて求めよ。
のときの解をすべて求めよ。 (2) 解が1つしかないようなnをすべて求めよ。
(3) 任意のnに対して解は少なくとも1つ存在し、かつ有限個しかないことを示せ。
この問題では、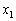 ,
,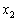 ,・・・,
,・・・,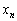 の大小関係が仮定されていないのですが、すべて異なる場合でも大小関係はn個の異なるものの順列
の大小関係が仮定されていないのですが、すべて異なる場合でも大小関係はn個の異なるものの順列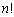 通りしか存在しないので、大小関係を仮定して考えるべきです。1つ解を求めてしまってから、あとで、並べ替えたものを列挙すればよいのです。というのは、整数問題では、大小関係を仮定することが強力な絞り込みの武器となることがあるからです。
通りしか存在しないので、大小関係を仮定して考えるべきです。1つ解を求めてしまってから、あとで、並べ替えたものを列挙すればよいのです。というのは、整数問題では、大小関係を仮定することが強力な絞り込みの武器となることがあるからです。
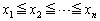 と仮定すると、
と仮定すると、
ですが、
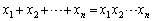 ・・・③
・・・③
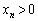 より、
より、
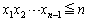 ・・・④
・・・④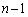 個の正整数の積がn以下ということで、チェックする範囲をかなり絞り込むことができるのです。
個の正整数の積がn以下ということで、チェックする範囲をかなり絞り込むことができるのです。
(1)の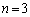 の場合が本問(1)です。並べ替えも入れて、
の場合が本問(1)です。並べ替えも入れて、 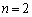 の場合は、
の場合は、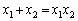 ・・・⑤
・・・⑤④より、
これをみたすのは、
の3通りの可能性しかありません。このうち⑤をみたすのは、
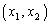 =
=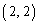 ......[答]
......[答]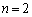 の場合、以下のような考え方もできます(こちらの方が普通の解法です)。
の場合、以下のような考え方もできます(こちらの方が普通の解法です)。
⑤を因数分解のような形に変形して、∴ 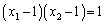 ・・・⑥
・・・⑥
これも、整数問題の基本ですが、(整数A)×(整数B)=(整数C) ・・・⑦
という形を作ると、AとBはCの約数に限定できるので、チェックする範囲を絞り込むことができます。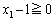 ,
,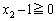 なので、⑥をみたすのは、
なので、⑥をみたすのは、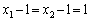 のときだけです。
のときだけです。
よって、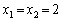 となります。
となります。
(2) 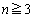 の場合に、n個の整数
の場合に、n個の整数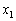 ,
,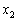 ,・・・,
,・・・,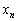 を2個の変数にできないか、2個の変数にしてしまえば、(1)の
を2個の変数にできないか、2個の変数にしてしまえば、(1)の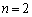 の別解の解法が使える、と、考えます。ちょっと遊びで、2個の変数
の別解の解法が使える、と、考えます。ちょっと遊びで、2個の変数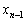 ,
,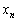 だけ残して、残りを全部
だけ残して、残りを全部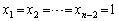 としてみます。③は、
としてみます。③は、 となります。左辺は1を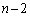 個足しているので、
個足しているので、 こうなれば、(1)の別解の解法が使えます。⑦の形になるように変形すると、
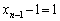 ,
,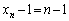
∴ 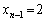 ,
,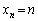
が③の1つの解を与えます。つまり、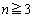 の場合、③には、
の場合、③には、 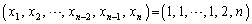 ・・・⑧
・・・⑧という解が存在するのです。この解には、3種類の整数、1と2とnが出てくるので、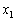 ,
,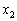 ,・・・,
,・・・,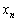 の並べ替えにより、複数の解を作ることができます。すなわち、
の並べ替えにより、複数の解を作ることができます。すなわち、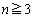 の場合には、2個以上の解が存在します。よって、解が1つしかないようなnは、(1)より、
の場合には、2個以上の解が存在します。よって、解が1つしかないようなnは、(1)より、 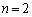 ......[答]
......[答]
(3) (1)の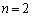 の場合と、
の場合と、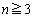 の場合の⑧により、任意のnに対して、③には、少なくとも1個の解が存在します。
の場合の⑧により、任意のnに対して、③には、少なくとも1個の解が存在します。 ③の解は④をみたしますが、④をみたす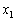 ,
,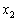 ,・・・,
,・・・,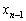 はすべて1以上でn以下の整数であって、
はすべて1以上でn以下の整数であって、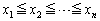 のとき
のとき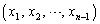 の組の個数は
の組の個数は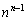 個以下です。
個以下です。
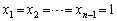 の場合には、
の場合には、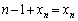 となるので、③はみたされません。
となるので、③はみたされません。
ということは、③の解の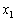 ,
,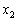 ,・・・,
,・・・,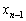 の中には2以上のものが含まれています。このとき、
の中には2以上のものが含まれています。このとき、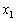 ,
,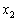 ,・・・,
,・・・,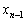 が決まれば、③により
が決まれば、③により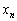 はただ1通りに決まります。
はただ1通りに決まります。
従って、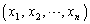 の組の個数も
の組の個数も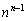 個以下です。
個以下です。
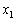 ,
,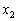 ,・・・,
,・・・,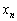 の大小関係は、n個の整数がすべて異なっていた場合の
の大小関係は、n個の整数がすべて異なっていた場合の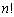 通り以下です。
通り以下です。
よって、③の解は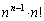 個以下であり、有限個しかありません。
個以下であり、有限個しかありません。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。