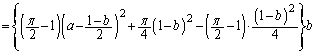���嗝�n���w'10�N�O��[1]
3�ӂ̒�����a��b��c �̒����̂��A������b��1�ӂ���]���Ƃ���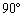 ��]������Ƃ��A�����̂��ʉ߂���_�S�̂����闧�̂�V�Ƃ���B
��]������Ƃ��A�����̂��ʉ߂���_�S�̂����闧�̂�V�Ƃ���B
(1) V�̑̐ς�a�Cb�Cc��p���ĕ\���B
(2) 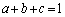 �̂Ƃ��AV�̑̐ς̂Ƃ肤��l�͈̔͂����߂�B
�̂Ƃ��AV�̑̐ς̂Ƃ肤��l�͈̔͂����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@����Ƃ��Ă͌ÓT�I��2�ϐ����̖��ł��B1�������Œ肷�邱�Ƃɂ��������܂��B
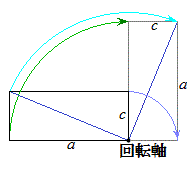 (1) ����V�̒�ʂ͉E�}�̂悤�ɂȂ��Ă��܂��B�������̒����`����]���̉���
(1) ����V�̒�ʂ͉E�}�̂悤�ɂȂ��Ă��܂��B�������̒����`����]���̉���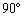 ��]�����Ƃ��ɒ����`���ʉ߂���̈�ł��B
��]�����Ƃ��ɒ����`���ʉ߂���̈�ł��B����V�̒�ʐ�S�́A���a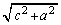 �̉~��
�̉~��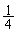 �ƁA���p���͂���2�ӂ�c�Ca�̒��p�O�p�`2�����킹�āA
�ƁA���p���͂���2�ӂ�c�Ca�̒��p�O�p�`2�����킹�āA ����V�̑̐�W�́A
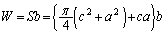 ......[��]
......[��]
(2) �@���Aa�Cb�Cc�͂�����������Ȃ̂ŁA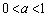 �C
�C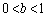 �C
�C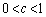 �ł��Ba�Cb�Cc��3�ϐ�����܂����A�W���F
�ł��Ba�Cb�Cc��3�ϐ�����܂����A�W���F 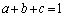 �@����@
�@����@������̂ŁA�����I��2�ϐ��ł��Bb���Œ肷��ƁA
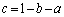 �@����A
�@����A���c���������邱�Ƃ��ł��܂��B�����ŁA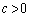 ���A
���A 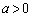 �ƍ��킹�āA
�ƍ��킹�āA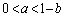 �@����B
�@����B(1)�̌��ʂɇA�������āA
b���Œ肵��W��a��2����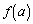 �ƌ���ƁA
�ƌ���ƁA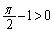 �ƇB���AW�́A
�ƇB���AW�́A 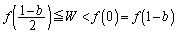 �@����C
�@����C�͈̔͂̒l���Ƃ蓾�܂��B
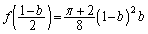 �C
�C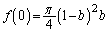
�����ŁA
�Ƃ����ƁA
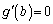 �Ƃ���ƁA
�Ƃ���ƁA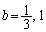
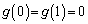 �C
�C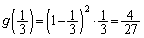
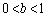 �C�����\���(3�����̑������Q��)�A
�C�����\���(3�����̑������Q��)�A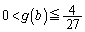
������Ab��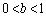 �͈̔͂œ������Ƃ��A
�͈̔͂œ������Ƃ��A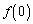 �C
�C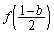 �̂Ƃ蓾��l�ɂ��āA
�̂Ƃ蓾��l�ɂ��āA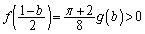 �C
�C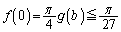 �@����D
�@����D�����藧���܂��B����āA�C���AV�̑̐�W�̂Ƃ肤��l�͈̔͂́A
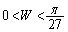 ......[��]
......[��]�NjL�D�C�C�D��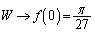 �ƂȂ�̂́A
�ƂȂ�̂́A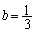 ����
����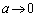 �܂���
�܂���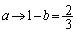 �̂Ƃ��ł��B
�̂Ƃ��ł��B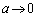 �̂Ƃ��ɂ�
�̂Ƃ��ɂ�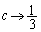 �C
�C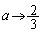 �̂Ƃ��ɂ�
�̂Ƃ��ɂ�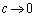 �ł��B�܂�A�����̂������Ȃ�A����2�ӂ��A
�ł��B�܂�A�����̂������Ȃ�A����2�ӂ��A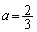 ����
����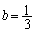 (���̂Ƃ�
(���̂Ƃ�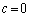 )�C�܂��́A
)�C�܂��́A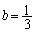 ����
����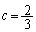 (���̂Ƃ�
(���̂Ƃ�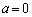 )�̒����`���ɋ߂Â��Ƃ��ł��B
)�̒����`���ɋ߂Â��Ƃ��ł��B
�D��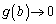 �ƂȂ�̂́A
�ƂȂ�̂́A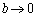 �܂���
�܂���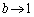 �̂Ƃ��ł��B
�̂Ƃ��ł��B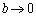 �̂Ƃ��Aa�Cc�ɂ�����炸�A
�̂Ƃ��Aa�Cc�ɂ�����炸�A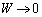 �ƂȂ�܂��B
�ƂȂ�܂��B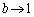 �̂Ƃ��A
�̂Ƃ��A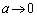 ����
����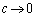 �ƂȂ�܂��B
�ƂȂ�܂��B
������A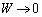 �ƂȂ�̂́A�����̂��A��b�̕����ɔ����Ȃ�(�����̂�����0��2�ӂ�a�Cc�̒����`�ɋ߂Â��B
�ƂȂ�̂́A�����̂��A��b�̕����ɔ����Ȃ�(�����̂�����0��2�ӂ�a�Cc�̒����`�ɋ߂Â��B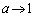 �܂���
�܂���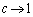 �̂Ƃ��ɒ���1�̖_����]����ꍇ���܂�)������1�̍ג����_�ɂȂ�Ƃ��ł��B
�̂Ƃ��ɒ���1�̖_����]����ꍇ���܂�)������1�̍ג����_�ɂȂ�Ƃ��ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B