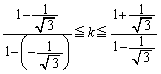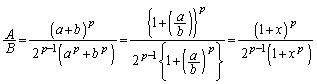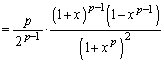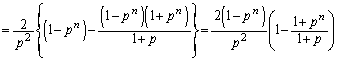������w���n2010�N�O�����w�������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[1]�@3�ӂ̒�����a��b��c �̒����̂��A������b��1�ӂ���]���Ƃ���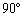 ��]������Ƃ��A�����̂��ʉ߂���_�S�̂����闧�̂�V�Ƃ���B
��]������Ƃ��A�����̂��ʉ߂���_�S�̂����闧�̂�V�Ƃ���B
(1) V�̑̐ς�a�Cb�Cc��p���ĕ\���B
(2) 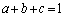 �̂Ƃ��AV�̑̐ς̂Ƃ肤��l�͈̔͂����߂�B
�̂Ƃ��AV�̑̐ς̂Ƃ肤��l�͈̔͂����߂�B
[��]
[2](1) ���ׂĂ̎��R��k�ɑ��āA���̕s�����������B
(2) 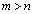 �ł���悤�Ȃ��ׂĂ̎��R��m��n�ɑ��āA���̕s�����������B
�ł���悤�Ȃ��ׂĂ̎��R��m��n�ɑ��āA���̕s�����������B [��]
[3]�@2�̔�L��R�C�{�[��30�A�R�C�������ŕ\�Ɨ������m��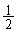 �ŏo��R�C��1����p�ӂ���Bx��0�ȏ�30�ȉ��̐����Ƃ���BL��x�CR��
�ŏo��R�C��1����p�ӂ���Bx��0�ȏ�30�ȉ��̐����Ƃ���BL��x�CR��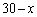 �̃{�[�������A���̑���(��)���J��Ԃ��B
�̃{�[�������A���̑���(��)���J��Ԃ��B
(��) ��L�ɓ����Ă���{�[���̌���z�Ƃ���B�R�C���𓊂��A�\���o��Δ�R���甠L�ɁA�����o��Δ�L���甠R�ɁA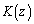 �̃{�[�����ڂ��B�������A
�̃{�[�����ڂ��B�������A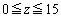 �̂Ƃ�
�̂Ƃ�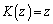 �C
�C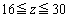 �̂Ƃ�
�̂Ƃ�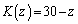 �Ƃ���B
�Ƃ���B
m��̑���̌�A��L�̃{�[���̌���30�ł���m����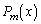 �Ƃ���B���Ƃ���
�Ƃ���B���Ƃ���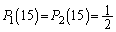 �ƂȂ�B�ȉ��̖�(1)�C(2)�C(3)�ɓ�����B
�ƂȂ�B�ȉ��̖�(1)�C(2)�C(3)�ɓ�����B
(1) 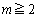 �̂Ƃ��Ax�ɑ��Ă��܂�y��I�сA
�̂Ƃ��Ax�ɑ��Ă��܂�y��I�сA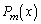 ��
��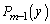 �ŕ\���B
�ŕ\���B (2) n�����R���Ƃ���Ƃ��A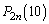 �����߂�B
�����߂�B (3) n�����R���Ƃ���Ƃ��A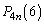 �����߂�B
�����߂�B [��]
[4]�@O�����_�Ƃ�����W���ʏ�̋Ȑ�
C�F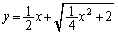
�ƁA���̏�̑��قȂ�2�_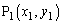 �C
�C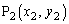 ���l����B
���l����B
(1) 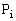 (
(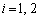 )��ʂ�x���ɕ��s�Ȓ����ƁA����
)��ʂ�x���ɕ��s�Ȓ����ƁA����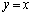 �Ƃ̌�_���A���ꂼ��
�Ƃ̌�_���A���ꂼ��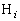 (
(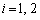 )�Ƃ���B���̂Ƃ�
)�Ƃ���B���̂Ƃ�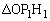 ��
��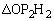 �̖ʐς͓��������Ƃ������B
�̖ʐς͓��������Ƃ������B (2) 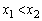 �Ƃ���B���̂Ƃ�C��
�Ƃ���B���̂Ƃ�C��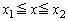 �͈̔͂ɂ��镔���ƁA����
�͈̔͂ɂ��镔���ƁA����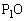 �C
�C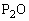 �Ƃň͂܂��}�`�̖ʐς��A
�Ƃň͂܂��}�`�̖ʐς��A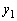 �C
�C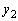 ��p���ĕ\���B
��p���ĕ\���B [��]
[5]�@C�a1�̉~���Ƃ��AA��C���1�_�Ƃ���B3�_P�CQ�CR��A������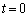 �ɏo�����AC����e�X���̑����ŁAP�CQ�͔����v���ɁAR�͎��v���ɁA����
�ɏo�����AC����e�X���̑����ŁAP�CQ�͔����v���ɁAR�͎��v���ɁA����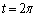 �܂œ����BP�CQ�CR�̑����́A���ꂼ��m�C1�C2�ł���Ƃ���B(���������āAQ��C�����傤�Lj������B)�������Am��
�܂œ����BP�CQ�CR�̑����́A���ꂼ��m�C1�C2�ł���Ƃ���B(���������āAQ��C�����傤�Lj������B)�������Am��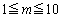 ���݂��������ł���B��PQR��PR���ΕӂƂ��钼�p�ӎO�p�`�ƂȂ�悤�ȑ���m�Ǝ���t�̑g�����ׂċ��߂�B
���݂��������ł���B��PQR��PR���ΕӂƂ��钼�p�ӎO�p�`�ƂȂ�悤�ȑ���m�Ǝ���t�̑g�����ׂċ��߂�B
[��]
[6]�@�l�ʑ�OABC�ɂ����āA4�̖ʂ͂��ׂč����ł���A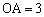 �C
�C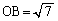 �C
�C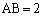 �ł���Ƃ���B�܂��A3�_O�CA�CB���܂ޕ��ʂ�L�Ƃ���B
�ł���Ƃ���B�܂��A3�_O�CA�CB���܂ޕ��ʂ�L�Ƃ���B
(1) �_C���畽��L�ɂ��낵�������̑���H�Ƃ����B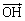 ��
��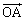 ��
��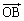 ��p���ĕ\���B
��p���ĕ\���B (2) 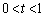 ���݂�������t�ɑ��āA����OA�COB�e�X��t�F
���݂�������t�ɑ��āA����OA�COB�e�X��t�F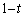 �ɓ�������_�����ꂼ��
�ɓ�������_�����ꂼ��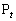 �C
�C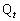 �Ƃ����B2�_
�Ƃ����B2�_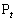 �C
�C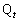 ��ʂ�A����L�ɐ����ȕ��ʂ�M�Ƃ���Ƃ��A����M�ɂ��l�ʑ�OABC�̐���̖ʐ�
��ʂ�A����L�ɐ����ȕ��ʂ�M�Ƃ���Ƃ��A����M�ɂ��l�ʑ�OABC�̐���̖ʐ�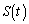 �����߂�B
�����߂�B (3) t��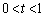 �͈̔͂��Ƃ��A
�͈̔͂��Ƃ��A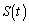 �̍ő�l�����߂�B
�̍ő�l�����߂�B [��]
�e�⌟��
[1](��������)�@2�ϐ����̍ő�E�ŏ����̉�@�ɂ́A�ȉ��̂悤�Ȃ��̂�����܂��B
(i) 2������2�����̏ꍇ�ɂ́A1�������������������܂��B 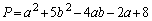 (a�Cb�͎���)�̍ŏ��l�����߂�̂ł���A�܂�a�ɂ��ĕ����������A�c����������b�ɂ��ĕ����������܂��B
(a�Cb�͎���)�̍ŏ��l�����߂�̂ł���A�܂�a�ɂ��ĕ����������A�c����������b�ɂ��ĕ����������܂��B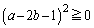 �C
�C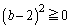 �Ȃ̂ŁAP�́A
�Ȃ̂ŁAP�́A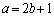 �C���A
�C���A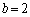 �C�܂�A
�C�܂�A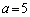 ����
����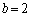 �̂Ƃ��ɍŏ��l3���Ƃ�܂��B
�̂Ƃ��ɍŏ��l3���Ƃ�܂��B
(ii) ����E���q���������̕����̌`�����Ă���ꍇ�ɂ�1�ϐ����ɒ����܂��B
2�ϐ��̕����ł��A����E���q�������ŁA��������v���Ă���ꍇ�ɂ́A2�ϐ��̔��V���ɕϐ��Ɏ�蒼����1�ϐ��̊��ɒ������Ƃ��ł��܂��B
�Ⴆ�A���嗝�H01�N[2]
�_A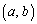 �͒��SO
�͒��SO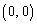 �C���a1�̉~�̓�������т��̎�����A�_P
�C���a1�̉~�̓�������т��̎�����A�_P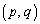 �͒��S
�͒��S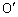
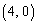 �C���a1�̉~�̓�������т��̎�����Ƃ���B���̂Ƃ��A
�C���a1�̉~�̓�������т��̎�����Ƃ���B���̂Ƃ��A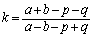 �Ƃ����B���̖₢�ɓ�����B
�Ƃ����B���̖₢�ɓ�����B
(1) ����AP�̌X����m�Ƃ���Bk��m��p���ĕ\���B
(2) k�̒l�̂Ƃ蓾��͈͂����߂�B
���@k��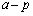 �C
�C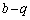 �ɂ��āA����A���q�Ƃ�1�����ł��B(1)�́A2�ϐ�
�ɂ��āA����A���q�Ƃ�1�����ł��B(1)�́A2�ϐ�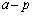 �C
�C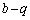 �̔���l����悤�ɑ����q���g�ł��B
�̔���l����悤�ɑ����q���g�ł��B (1) 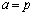 �ɂ͂Ȃ蓾�Ȃ��̂ŁA����BP�̌X���F
�ɂ͂Ȃ蓾�Ȃ��̂ŁA����BP�̌X���F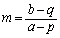 (�����̕��������Q��)���Ak�̎��̕���E���q��
(�����̕��������Q��)���Ak�̎��̕���E���q��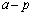 �Ŋ����āA
�Ŋ����āA 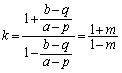 ......[��]
......[��](2) 2�~�̒��SO�C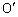 �̒��_M��
�̒��_M��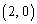 �ł��B����AP�����낢��Ɠ������Ă݂�ƁA����AP��M��ʉ߂��Ă��A2�~�ɐڂ���Ƃ���m���ő�E�ŏ��ƂȂ邱�Ƃ��킩��܂��B���̂Ƃ��AA�CP�͐ړ_�ɂȂ�A
�ł��B����AP�����낢��Ɠ������Ă݂�ƁA����AP��M��ʉ߂��Ă��A2�~�ɐڂ���Ƃ���m���ő�E�ŏ��ƂȂ邱�Ƃ��킩��܂��B���̂Ƃ��AA�CP�͐ړ_�ɂȂ�A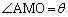 �Ƃ��āA
�Ƃ��āA ���A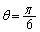 �C
�C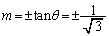 �ƂȂ�܂��B�]���āAm�̂Ƃ肤��l�͈̔͂́A
�ƂȂ�܂��B�]���āAm�̂Ƃ肤��l�͈̔͂́A 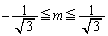 �@����@
�@����@(1)�̌��ʂ��A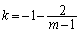
���̃O���t�́A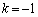 �C
�C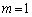 ��Q�ߐ��Ƃ���o�Ȑ��ł��B�@�͈̔͂ɂ�����k��m�̑������ŁA
��Q�ߐ��Ƃ���o�Ȑ��ł��B�@�͈̔͂ɂ�����k��m�̑������ŁA �� 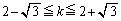 ......[��]
......[��] ���̓��H��99�N[1]�����l�̔��z�ʼnł��܂��B
���̎���a�Cb�Cp�ɑ��āA
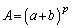 ��
��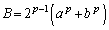
�̑召�W�ׂ�B
���@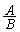 ��a�Cb��2�ϐ����ł����A����E���q�Ƃ�p���̓������Ȃ̂ŁA
��a�Cb��2�ϐ����ł����A����E���q�Ƃ�p���̓������Ȃ̂ŁA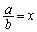 (
(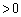 )��1�ϐ����ƍl���邱�Ƃ��ł��܂��B
)��1�ϐ����ƍl���邱�Ƃ��ł��܂��B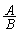 �̕���E���q��
�̕���E���q��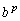 �Ŋ����āA
�Ŋ����āA 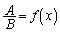 �Ƃ��āA
�Ƃ��āA(a) 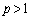 �̂Ƃ��A
�̂Ƃ��A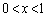 ��
��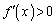 �C
�C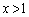 ��
��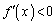 ���A
���A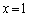 �ɂ�����
�ɂ�����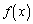 �ő�ŁA
�ő�ŁA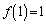 ���A
���A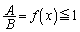 (�s�����̓�����
(�s�����̓�����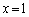 �̂Ƃ�)
�̂Ƃ�) (b) 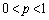 �̂Ƃ��A
�̂Ƃ��A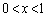 ��
��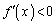 �C
�C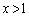 ��
��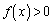 ���A
���A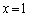 �ɂ�����
�ɂ�����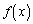 �ŏ��ŁA
�ŏ��ŁA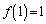 ���A
���A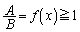 (�s�����̓�����
(�s�����̓�����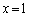 �̂Ƃ�)
�̂Ƃ�) (c) 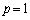 �̂Ƃ��A
�̂Ƃ��A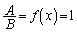
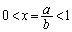 �̂Ƃ�
�̂Ƃ�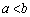 �C
�C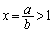 �̂Ƃ�
�̂Ƃ�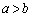 �C
�C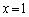 �̂Ƃ�
�̂Ƃ�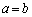 �Ȃ̂ŁA(a)(b)(c)���A
�Ȃ̂ŁA(a)(b)(c)���A
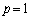 �܂���
�܂���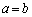 �̂Ƃ�
�̂Ƃ�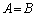 �C
�C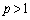 ����
����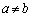 �̂Ƃ�
�̂Ƃ�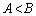 �C
�C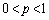 ����
����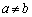 �̂Ƃ�
�̂Ƃ�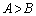 ......[��]
......[��]
(iii) 1�������Œ肵�đ����̕�����ω������A�ő�ŏ����Œ肵�������̊��Ƃ��ċ��߂Ă����A�͂��߂ɌŒ肵�Ă�������������ɓ������čő�ŏ������߂܂��B
�Ⴆ�A����83�N[3]�ł́A
���ʏ�ɓ_O�𒆐S�Ƃ��锼�a1�̉~C������B�܂��A���̕��ʏ��O�ƈقȂ�_A��ʂ��Ē���OA�Ɛ����ȋ�Ԓ���l������A���ʂƂ̂Ȃ��p��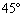 �ł���B���̂Ƃ��A�~C�ƒ���l�̊Ԃ̍ŒZ�������A2�_O�CA�Ԃ̋���a�ŕ\���B
�ł���B���̂Ƃ��A�~C�ƒ���l�̊Ԃ̍ŒZ�������A2�_O�CA�Ԃ̋���a�ŕ\���B
���@�_O�����_�Ƃ��āA����OA�̕�����x���A���ʏ�ɒ���OA�Ɛ����ȕ�����y���A���̕��ʂƐ�����z�����Ƃ�܂��B�~��C��̓_P�̍��W��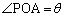 �Ƃ��āA
�Ƃ��āA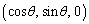 �ƕ\���܂��B����l�̕����x�N�g����
�ƕ\���܂��B����l�̕����x�N�g����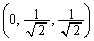 �Ƃ��܂��B
�Ƃ��܂��B ���D����l�̕����x�N�g���́A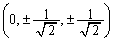 �̕����̎�����4�ʂ�̉\��������܂����A�ǂ���Ƃ��Ă����ʂɕς��͂���܂���B
�̕����̎�����4�ʂ�̉\��������܂����A�ǂ���Ƃ��Ă����ʂɕς��͂���܂���B ����l��A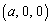 ��ʂ�̂ŁAl��̓_Q�̍��W
��ʂ�̂ŁAl��̓_Q�̍��W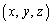 �́At�������Ƃ��āA
�́At�������Ƃ��āA �ƕ\���܂��B
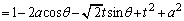
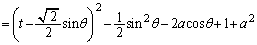
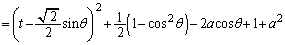
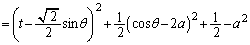 �@(
�@(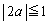 �Ƃ��������t���Ȃ�(i)�̏ꍇ�ɂȂ�܂����A
�Ƃ��������t���Ȃ�(i)�̏ꍇ�ɂȂ�܂����A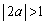 �Ƃ������Ƃ����蓾��̂ŁA
�Ƃ������Ƃ����蓾��̂ŁA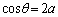 �̂Ƃ��ɍŏ��l���Ƃ�Ƃ͌���܂���)
�̂Ƃ��ɍŏ��l���Ƃ�Ƃ͌���܂���)t��θ ��2�ϐ����ɂȂ�܂����A�܂�θ ���Œ肵��t��2�����ƌ���ƁA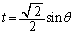 �̂Ƃ��ɍŏ��ƂȂ�A���̂Ƃ��A
�̂Ƃ��ɍŏ��ƂȂ�A���̂Ƃ��A ���x��θ �����ƁA�����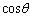 �Ɋւ���2�����ƌ��邱�Ƃ��ł��āA
�Ɋւ���2�����ƌ��邱�Ƃ��ł��āA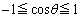 ���A
���A �ƂȂ�܂��B����āA�~C�ƒ���l�̊Ԃ̍ŒZ�����́A
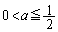 �̂Ƃ�
�̂Ƃ�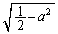 �C
�C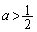 �̂Ƃ�
�̂Ƃ�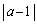 ......[��]����99�N���[2]�ł́A
......[��]����99�N���[2]�ł́A
α�Cβ�Cγ��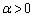 �C
�C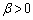 �C
�C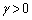 �C
�C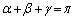 �������̂Ƃ���B���̂Ƃ��A
�������̂Ƃ���B���̂Ƃ��A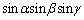 �̍ő�l�����߂�B
�̍ő�l�����߂�B
���@α�Cβ�Cγ��3�ϐ�������܂����A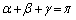 �Ƃ����W������̂Ŏ����I��2�ϐ��ł��B�܂��A3�ϐ��Ƃ��A
�Ƃ����W������̂Ŏ����I��2�ϐ��ł��B�܂��A3�ϐ��Ƃ��A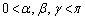 �ł��B
�ł��B �����ŁAγ ���Œ肵��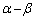 �����ƁA
�����ƁA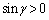 �C
�C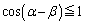 ���A
���A 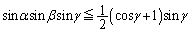 �@(�s�����̓�����
�@(�s�����̓�����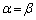 �̂Ƃ��ɐ���)
�̂Ƃ��ɐ���)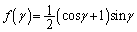 �Ƃ����ƁA
�Ƃ����ƁA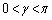 �ɂ����ẮA
�ɂ����ẮA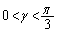 �̂Ƃ�
�̂Ƃ�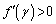 �C
�C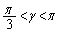 �̂Ƃ�
�̂Ƃ�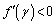 ���A
���A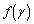 �̍ő�l��
�̍ő�l��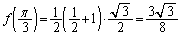 (���̑������Q��)�ŁA
(���̑������Q��)�ŁA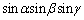 �̍ő�l���A
�̍ő�l���A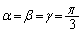 �̂Ƃ���
�̂Ƃ���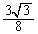 ......[��]
......[��]
[2](��������)�@�ɂ������܂������A07�N�O��[6]�����Ղ����������ł��B�����07�N�O��[6]�Ɣ�ׂ�ƁA�{��(1)�̃A�C�f�A�́A�O���t��`���⏕�������낢��ƈ����Ă݂�Ύ������ł��C�Â��邾�낤�Ǝv���܂��B�����A�C�Â��Ȃ��A�ƁA����������������̂ł���A���R�ƌ���m��̐����őË����Ă��܂�Ȃ��ŁA�g�̉��̂��Ƃ���ׂ����H�v���Â炷���Ƃ��l���Ă݂Ă��������B
�Y�ꕨ���������́A�Y�ꕨ�`�F�b�N�E�V�[�g��p�ӂ��ĊO�o����O�Ƀ`�F�b�N����悤�ɂ��܂��傤�B
�������₷���Q�Ăӂ��߂��ă~�X�𗐔�������́A�����悤�Ȃ��Ƃ��N�����Ƃ��Ɉ�x�傫���[�ċz����悤�ɂ��܂��傤�B
�҂����킹�̎��������Ȃ����́A����I�ȍs���ɗv���鎞�ԂׂāA�҂����킹��������t�Z���ĕ����݂ŃX�P�W���[�����O�����Ă݂܂��傤�B
���w�̉�@�p�^�[���ɏK�n���邾���łȂ��A�����������X�̍H�v������S�������A�������ł��A���낢��Ǝ��s���낵�A�A�C�f�A���Ђ˂�o���ӗ~�ɂȂ���͂��ł��B
�{��(2)�̃|�C���g�́A���̕s�����D�F
�ŁA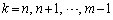 �Ƃ�������ӁX�������킹�邱�Ƃɂ���܂��B�אڂ��鍀�̘a�̒��ɑł������������̂������āA�a�̐擪�Ɩ����������c��A���ʂ̌`��������A�Ƃ����Z�I���g���܂��B�܂��A�{��ł́A(1)�œ���ꂽ�`��P���ɉ������킹��̂ł͂Ȃ��A�ړI�̌`���ł���悤�Ɏ��ό`���Ȃ�������Ȃ��A�Ƃ����Ƃ��낪�ǂɂȂ��Ă��܂��B���������_�́A91�N�O��[6]��A����08�N�O��[3]�Ȃǂɂ������܂��B��Ђ˂�ōς܂��ɁA������Ђ˂�A����ɓ�Ђ˂肷��A�Ƃ����S�苭�����v������܂��B������ƍs���l�܂����A�Ƃ��������Œ��߂Ă��܂킸�ɁA���Ƃ�����������o���Ȃ����̂��A�����炪���߂Ȃ炠����A����������߂Ȃ炳��ɂ��̌������A�Ƃ��������łǂ��܂ł��˂��l�߂Ă����C�������K�v�ł��B�������A���w�̓��Ɏ����玟�ւƒ��킵�Ă����A�Ƃ������w�I�Z�I�̑��ʂ������łȂ��A���퐶���̒��ŕs���s���̐��_��b���܂��傤�B
�Ƃ�������ӁX�������킹�邱�Ƃɂ���܂��B�אڂ��鍀�̘a�̒��ɑł������������̂������āA�a�̐擪�Ɩ����������c��A���ʂ̌`��������A�Ƃ����Z�I���g���܂��B�܂��A�{��ł́A(1)�œ���ꂽ�`��P���ɉ������킹��̂ł͂Ȃ��A�ړI�̌`���ł���悤�Ɏ��ό`���Ȃ�������Ȃ��A�Ƃ����Ƃ��낪�ǂɂȂ��Ă��܂��B���������_�́A91�N�O��[6]��A����08�N�O��[3]�Ȃǂɂ������܂��B��Ђ˂�ōς܂��ɁA������Ђ˂�A����ɓ�Ђ˂肷��A�Ƃ����S�苭�����v������܂��B������ƍs���l�܂����A�Ƃ��������Œ��߂Ă��܂킸�ɁA���Ƃ�����������o���Ȃ����̂��A�����炪���߂Ȃ炠����A����������߂Ȃ炳��ɂ��̌������A�Ƃ��������łǂ��܂ł��˂��l�߂Ă����C�������K�v�ł��B�������A���w�̓��Ɏ����玟�ւƒ��킵�Ă����A�Ƃ������w�I�Z�I�̑��ʂ������łȂ��A���퐶���̒��ŕs���s���̐��_��b���܂��傤�B
[3](��������)�@(1)��������ăp�X���A(2)�C(3)����������A�Ƃ������Ƃɂ���Γ��ł͂Ȃ����A���i�̂��߂ɂ͂��̕����������Ǝv���܂��B���ƌ����Ă�(1)�̖�蕶�̈Ӗ�����Ƃ��낪����ł��B�o��҂��q���g�̂���Ŗ�蕶�ɏ����Ă��邱�Ƃ��A���ɂƂ��Ă͖��f�Ȃ��ƂɂȂ��Ă���̂ł����A���炩���ߓ������𑽐��̐l�Ƀ��j�^�[���Ă��炤�킯�ɂ������Ȃ��̂ŁA�����������Ƃ͋N���蓾��ƍl���Ă��������ǂ������ł��B
(1)���ȉ��̉ߋ���̌o��������A�ŏ���1��̑O��̊W�ׂ�Ƃ����A�C�f�A�͎��`�}����v�����Ȃ����Ƃ͂Ȃ��Ǝv���܂��B�ł����A���\�N�����ߋ�������Ă����͕̂��ʂ̎��ł͖������Ǝv���܂��B�܂��A���퐶�����琔�w�ȊO�̉ۑ�ɑ��Ă��A�펯�I�Ȕ��z�ɂƂ��ꂸ�Ɋ�ȃA�C�f�A���v�������ׂ�A�Ƃ������Ƃ�����Ă�����łȂ��ƁA�������ł��傤�B
���āA�ɏ���������84�N[5]�͈ȉ��̖��ł��B�{��(2)�C(3)�����̂Ƃ��Ɣ�ׂ�ƁA������̕�����������ł��B
�e���ゲ�ƂɁA�e�̂��A���̌̂Ƃ͓Ɨ��ɁA�m��p��1�A�m��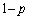 ��2�̐V�����̂����̐���Ɏc���A���ꎩ�g�͏��ł���זE������B���܁A��0�����1�ł������זE���A��n�����m�ƂȂ�m�����A
��2�̐V�����̂����̐���Ɏc���A���ꎩ�g�͏��ł���זE������B���܁A��0�����1�ł������זE���A��n�����m�ƂȂ�m�����A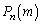 �Ə������Ƃɂ��悤�Bn�����R���Ƃ���Ƃ��A
�Ə������Ƃɂ��悤�Bn�����R���Ƃ���Ƃ��A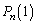 �C
�C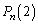 �C
�C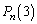 �����߂�B
�����߂�B
(iii) 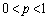 �̂Ƃ�
�̂Ƃ� ��0���ォ��m��p�ōזE1��(��0����Ɠ�����)�ɂȂ�A�ȍ~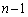 ����ōזE��1�ɂȂ�m����
����ōזE��1�ɂȂ�m����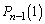 �C��U�זE��2�ȏ�ɂȂ��Ă��܂��A�זE1�̏ɂ͖߂�Ȃ��̂ŁA
�C��U�זE��2�ȏ�ɂȂ��Ă��܂��A�זE1�̏ɂ͖߂�Ȃ��̂ŁA ������A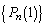 �́A����
�́A����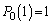 �C����p�̓��䐔��ŁA
�C����p�̓��䐔��ŁA 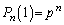 ......[��]
......[��]��0���ォ��m��p�ōזE1��(��0����Ɠ�����)�ɂȂ�A�ȍ~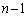 ����ōזE��2�ɂȂ�m����
����ōזE��2�ɂȂ�m����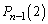 �C��0���ォ��m��
�C��0���ォ��m��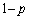 �ōזE��2�ɂȂ��Ă��܂��ƁA�ȍ~
�ōזE��2�ɂȂ��Ă��܂��ƁA�ȍ~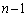 ����ł́A2�̍זE�ɂ��āA�m��p��1�̍זE����1�̍זE�������邾���ɂȂ�̂ŁA
����ł́A2�̍זE�ɂ��āA�m��p��1�̍זE����1�̍זE�������邾���ɂȂ�̂ŁA 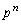 �Ŋ����āA
�Ŋ����āA������A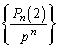 �̊K������
�̊K������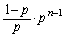 �C�ƌ��āA
�C�ƌ��āA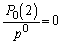 ���A
���A �� 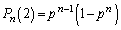 ......[��]��0����ōזE��2����Ƃ��āA��n����ōזE��3�ɂȂ�m����
......[��]��0����ōזE��2����Ƃ��āA��n����ōזE��3�ɂȂ�m����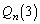 �Ƃ��܂��B
�Ƃ��܂��B
��0����ōזE��1�̏ŁA��0���ォ��m��p�ōזE1�ɂȂ�A�ȍ~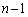 ����ōזE��3�ɂȂ�m����
����ōזE��3�ɂȂ�m����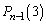 �C��0���ォ��m��
�C��0���ォ��m��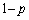 �ōזE��2�ɂȂ��Ă��܂��ƁA�ȍ~
�ōזE��2�ɂȂ��Ă��܂��ƁA�ȍ~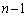 ����ōזE��3�ɂȂ�m����
����ōזE��3�ɂȂ�m����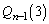 �ɂȂ�̂ŁA
�ɂȂ�̂ŁA 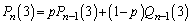 �@����@
�@����@��0����ōזE��2����Ƃ��A�m��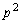 �ōזE��2�̂܂܂ɂȂ�A�ȍ~
�ōזE��2�̂܂܂ɂȂ�A�ȍ~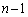 ����ōזE��3�ɂȂ�m����
����ōזE��3�ɂȂ�m����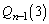 �C��0���ォ��m��
�C��0���ォ��m��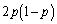 �ōזE��3�ɂȂ��Ă��܂��ƁA�ȍ~
�ōזE��3�ɂȂ��Ă��܂��ƁA�ȍ~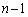 ����ł́A3�̍זE�ɂ��āA�m��p��1�̍זE����1�̍זE�������邾���ɂȂ�̂ŁA
����ł́A3�̍זE�ɂ��āA�m��p��1�̍זE����1�̍זE�������邾���ɂȂ�̂ŁA 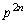 �Ŋ����āA
�Ŋ����āA������A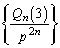 �̊K������
�̊K������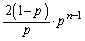 �C�ƌ��āA
�C�ƌ��āA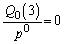 ���A
���A �� 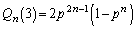 �@�ɑ�����āA
�@�ɑ�����āA 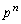 �Ŋ����āA
�Ŋ����āA������A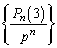 �̊K������
�̊K������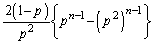 �C�ƌ��āA
�C�ƌ��āA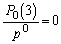 ���A
���A �� 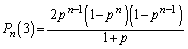 ......[��]
......[��]
����90�N�O��[6]�͈ȉ��̖��ł��B������́A�{��(2)�C(3)�Ɠ����x�ł��B
��̃T�C�R���𑱂��ē����āA�ŏ���n��ɏo���ڂ̐������̏����̂܂����_�ȉ��ɕ��ׂĂł��������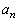 �Ƃ����B���Ƃ��A�o���ڂ̐���5�C2�C6�C����ł���A
�Ƃ����B���Ƃ��A�o���ڂ̐���5�C2�C6�C����ł���A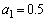 �C
�C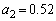 �C
�C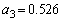 �C����ł���B����α�ɑ���
�C����ł���B����α�ɑ���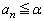 �ƂȂ�m����
�ƂȂ�m����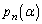 �Ƃ����B
�Ƃ����B
(1) 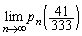 �����߂�B
�����߂�B (2) 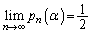 �ƂȂ�̂�α���ǂ̂悤�Ȕ͈͂ɂ���Ƃ����B
�ƂȂ�̂�α���ǂ̂悤�Ȕ͈͂ɂ���Ƃ����B
��(1) 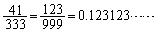 �ł��B
�ł��B 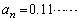 �C
�C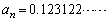 �ȂǂƂȂ�A
�ȂǂƂȂ�A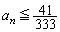 �ƂȂ�킯�ł����A3�Ƃɓ������Ƃ��J��Ԃ���邱�Ƃɒ��ڂ��܂��Bk�����R���Ƃ��āA�T�C�R����
�ƂȂ�킯�ł����A3�Ƃɓ������Ƃ��J��Ԃ���邱�Ƃɒ��ڂ��܂��Bk�����R���Ƃ��āA�T�C�R����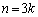 �����Ƃ���
�����Ƃ���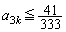 �ƂȂ�m��
�ƂȂ�m��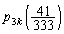 ���l���܂��B
���l���܂��B
�T�C�R����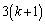 ����
����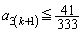 �ƂȂ�(�m��
�ƂȂ�(�m��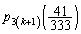 )�̂́A1��ڂ�1���o��(�m��
)�̂́A1��ڂ�1���o��(�m��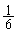 )�A���A2��ڂ�1���o��(�m��
)�A���A2��ڂ�1���o��(�m��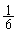 )���A�܂��́A2���o�āA�Ȃ����A2��ڂ�2���o��(�m��
)���A�܂��́A2���o�āA�Ȃ����A2��ڂ�2���o��(�m��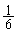 )�Ƃ��́A3��ڂ�1��2���o��(�m��
)�Ƃ��́A3��ڂ�1��2���o��(�m��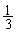 )���A�܂��́A3���o���Ƃ��ŁA3��ڂ�3���o��(�m��
)���A�܂��́A3���o���Ƃ��ŁA3��ڂ�3���o��(�m��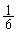 )�Ƃ��ɂ́A�c��
)�Ƃ��ɂ́A�c��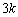 ���
���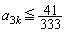 �ƂȂ�(�m��
�ƂȂ�(�m��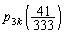 )�Ƃ��ł��B����āA
)�Ƃ��ł��B����āA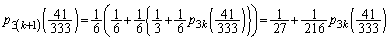 ��
�� 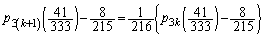
������A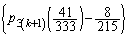 �́A����
�́A����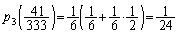 �C����
�C����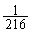 �̓��䐔��ŁA
�̓��䐔��ŁA 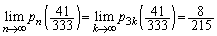 ......[��]
......[��](2) 1��ڂ�1��2��3���o��m����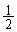 �ł��B���̂Ƃ���n��T�C�R���𓊂��đ�ӂ̂悤�ɂ��Ăł������
�ł��B���̂Ƃ���n��T�C�R���𓊂��đ�ӂ̂悤�ɂ��Ăł������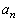 �́A1��ڂ�3���o�ĈȌ�6���o�����Ăł������
�́A1��ڂ�3���o�ĈȌ�6���o�����Ăł������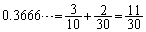 �ȉ��ł��B�܂��A�T�C�R���̖ڂ�1�`6�����Ȃ��̂ŁA
�ȉ��ł��B�܂��A�T�C�R���̖ڂ�1�`6�����Ȃ��̂ŁA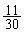 ���傫���A1��ڂ�4���o�ĈȌ�1���o�����Ăł������
���傫���A1��ڂ�4���o�ĈȌ�1���o�����Ăł������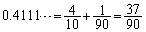 �����̎������ł��邱�Ƃ͂���܂���B����āA
�����̎������ł��邱�Ƃ͂���܂���B����āA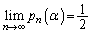 �ƂȂ�α�́A
�ƂȂ�α�́A 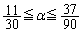 ......[��]
......[��]
[4](��������)�@�{��́A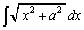 �Ƃ����`�̐ϕ��v�Z�Ɋւ���Z�I��w�i�Ƃ������ł��B
�Ƃ����`�̐ϕ��v�Z�Ɋւ���Z�I��w�i�Ƃ������ł��B
�{�N���嗝�H[4]�ł́A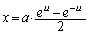 �Ƃ����āA
�Ƃ����āA
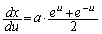 �C
�C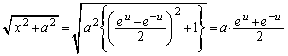
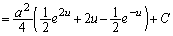 �@(C�F�ϕ��萔)
�@(C�F�ϕ��萔)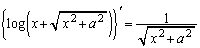 �𗘗p���āA�ȉ��̂悤�ɕ����ϕ��𑣂��U�����悭�������܂��B
�𗘗p���āA�ȉ��̂悤�ɕ����ϕ��𑣂��U�����悭�������܂��B
�� 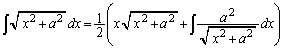
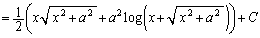 �@(C�F�ϕ��萔)
�@(C�F�ϕ��萔)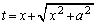 �Ƃ����u���ϕ���������@���m���Ă��܂��B
�Ƃ����u���ϕ���������@���m���Ă��܂��B
���A
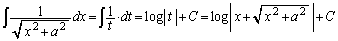 �@(C�F�ϕ��萔)
�@(C�F�ϕ��萔)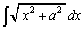 �̏ꍇ�͏��X�H�v�����āA
�̏ꍇ�͏��X�H�v�����āA
���A
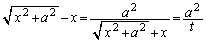 �C
�C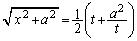
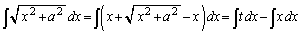 �@(�������݂��ł�)
�@(�������݂��ł�)
���āA����Y�܂���₪���o�̓��嗝�n�ł��A������Z�I����g����悤�Ȗ�肪���N1�`2��o�肳��Ă��܂��B2010�N�x�ł́A�{�₪�����������ɓ�����܂��B��(2)�ł́A�Z�I�ɑ��炸�f���ȍl�����ł���Ă���܂����A���܂����̂ł���A�ȉ��̂悤�ȁA�t�����l�����@�̕����e�Ղɖʐς����߂邱�Ƃ��ł��܂��B
�̐}�ŁA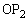 ��
��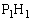 �̌�_��Q�Ƃ���ƁA(1)���A
�̌�_��Q�Ƃ���ƁA(1)���A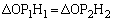 �Ȃ̂ŁA
�Ȃ̂ŁA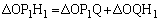 �C
�C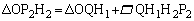 ���A
���A
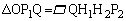 �@����@
�@����@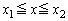 �͈̔͂ɂ��镔����
�͈̔͂ɂ��镔����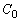 �Ƃ��܂��B
�Ƃ��܂��B
���ƂȂ��Ă���ʐρA�܂�A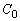 �Ɛ���
�Ɛ���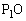 �C
�C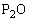 �Ƃň͂܂��}�`�̖ʐ�S�́A
�Ƃň͂܂��}�`�̖ʐ�S�́A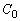 �Ɛ���
�Ɛ���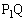 �C
�C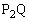 �ň͂܂�镔���̖ʐς�
�ň͂܂�镔���̖ʐς�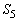 �Ƃ��āA�@���A
�Ƃ��āA�@���A
�ƂȂ�A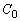 �ƒ���
�ƒ���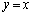 �C����
�C����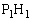 �C
�C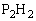 �Ɉ͂܂ꂽ�����̖ʐςɓ������Ȃ�܂��B����āA�Ȑ�C��^�������
�Ɉ͂܂ꂽ�����̖ʐςɓ������Ȃ�܂��B����āA�Ȑ�C��^�������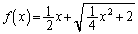 �C���̋t����
�C���̋t����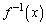 �Ƃ��āA�ʐ�S�́Ay�����̒�ϕ��F
�Ƃ��āA�ʐ�S�́Ay�����̒�ϕ��F
�ŗ^�����܂��B���̇D���F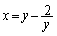 �𗘗p����A
�𗘗p����A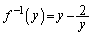 ���A
���A
�ƂȂ�܂��B
�ŏ������Ax�����̒�ϕ��̂܂�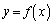 �Œu���ϕ����s���l�����́A������قɂ��܂����A�~�������ɂ��y���̉��̉�]�̂̌����̏ؖ��Ȃǂɏo�Ă���l�����Ƌ��ʂ̂��̂ł��B
�Œu���ϕ����s���l�����́A������قɂ��܂����A�~�������ɂ��y���̉��̉�]�̂̌����̏ؖ��Ȃǂɏo�Ă���l�����Ƌ��ʂ̂��̂ł��B
�Ⴆ�A����89�N[5]�F
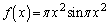 �Ƃ���B
�Ƃ���B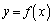 �̃O���t��
�̃O���t��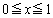 �̕�����x���Ƃň͂܂ꂽ�}�`��y���̂܂��ɉ�]�����Ăł��闧�̂̑̐�V�́A
�̕�����x���Ƃň͂܂ꂽ�}�`��y���̂܂��ɉ�]�����Ăł��闧�̂̑̐�V�́A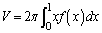 �ŗ^�����邱�Ƃ������A���̒l�����߂�B
�ŗ^�����邱�Ƃ������A���̒l�����߂�B
���@��������̉~���ɕ������Đϕ����邱�Ƃ�}�`�I�ɐ������邱�Ƃ��\�ł����A�����ł́A�v�Z�ł���Ă݂܂��B
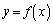 ��
��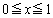 �ɂ�����
�ɂ�����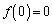 �����U��������
�����U��������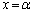 (
(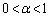 )�ŋɑ�l
)�ŋɑ�l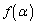 ���Ƃ�
���Ƃ�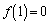 �܂Ō���������ł��B�������̕����̋t����
�܂Ō���������ł��B�������̕����̋t����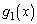 �C�������̕����̋t����
�C�������̕����̋t����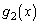 �Ƃ���ƁA
�Ƃ���ƁA
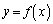 �ɑ��āA
�ɑ��āA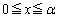 �̂Ƃ�
�̂Ƃ�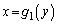 �C
�C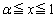 �̂Ƃ�
�̂Ƃ�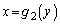 �ł��B
�ł��B
�e��`��ɂ�����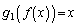 �C
�C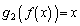 �C�܂��A
�C�܂��A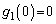 �C
�C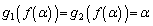 �C
�C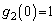 �ɒ��ӂ��Ă��������B
�ɒ��ӂ��Ă��������B
y���̉��̉�]�̂̑̐ςȂ̂ŁA���ʂ͊O����������������Ay�����ɐϕ����āA
�Ƃ���킯�ł����A���̖��ŗ^�����Ă���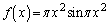 �ł͋t�������߂��Ȃ��̂ŁA
�ł͋t�������߂��Ȃ��̂ŁA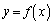 �ƒu�����Đϕ����s���܂��B
�ƒu�����Đϕ����s���܂��B
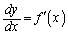 ���A
���A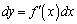
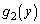 �̐ϕ��ł́Ay�F
�̐ϕ��ł́Ay�F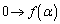 �̂Ƃ��Ax�F
�̂Ƃ��Ax�F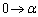
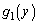 �̐ϕ��ł́Ay�F
�̐ϕ��ł́Ay�F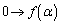 �̂Ƃ��Ax�F
�̂Ƃ��Ax�F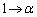
�����ŕ����ϕ��@��p���āA
�ƂȂ�܂��B���̌��ʂ𗘗p���āA
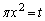 �Ƃ����ƁA
�Ƃ����ƁA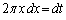
x�F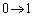 �̂Ƃ��At�F
�̂Ƃ��At�F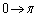
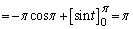 ......[��]
......[��]
[5](��������)�@�{��́A���ɉ��悤�Ǝv���A���N�₩�ȉ�@���H�v���邱�Ƃ��\�Ȗ��ł����A���́A�����������́A�������Ԃ������Ă����S�Ȏ菇�Ŋm���ɉ����Ă�����������I���Ǝv���܂��B
�ł́A�V���~�Ԃ��Œ��ׂ�k��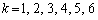 ��6�ʂ�Ɍ����Ē��ׂ�A�Ƃ������j�ŏ����Ă���܂����A
��6�ʂ�Ɍ����Ē��ׂ�A�Ƃ������j�ŏ����Ă���܂����A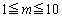 �Ƃ�������̒���
�Ƃ�������̒���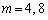 �Ɍ�����A�Ƃ������j�Ői�߂A2�ʂ�ł��݂܂�(���̇B�������Ȃ���e���H�v���Ă݂Ă�������)�B
�Ɍ�����A�Ƃ������j�Ői�߂A2�ʂ�ł��݂܂�(���̇B�������Ȃ���e���H�v���Ă݂Ă�������)�B
�������ŁA2�ʂ�̏ꍇ�����ł��މ�@���v���������ʼn���悢���A6�ʂ�̏ꍇ�������K�v�ɂȂ��Ă��܂��Ă�����ʼn���悢�̂ł��B6�ʂ��2�ʂ�ł��܂Ȃ����A�Ɛ[�ǂ����Ă��܂��ƁA6�ʂ�̏ꍇ�����ʼn��鎞�Ԃ̕����Z�������A�Ƃ������ƂɂȂ肩�˂܂���B
�����A�����A50�ʂ�ׂȂ�������Ȃ��̂��Ƃ�����A�����10�ʂ���x�ɂł��Ȃ����A�H�v����K�v�͂���ł��傤�B
�������ł́A�����������ɂ߂��d�v�ŁA����I�Ȋw�K�̒��ŁA���̉�@�ʼn����Ƃǂꂭ�炢�̎��Ԃ������邩�A�܂��A��@���v�����̂ɂǂꂭ�炢�̎��Ԃ������邩�A�Ƃ������ӎ������悤�ɂ��āA�͎�����Ƃ��ȂǂɎ����Ă݂�悤�ɂ��Ă��������B
�{��́A[3]�قǂł͂���܂��A��蕶������Ȃ葦�A�������Ɣ��f�ł���킯�ł͂Ȃ��A��蕶��lj����ĉ����l����ׂ����A�Ƃ����Ƃ��납��n�߂�K�v������܂��B���w�̓������͕����̓������ɔ�ׂ��ꡂ��ɒZ���ł����A�o��⎍��ǂ�ŏ�i���v�������ׂ�̂Ƌ��ʂ���C���[�W�͂��K�v�ŁA���吔�w�ł͓��Ɍ����邱�Ƃł��B���H�n��֑��ڎw�������́A����̎��ƒ��ɁA�o��ȂNJW�Ȃ��Ǝv������ŋ���������Ă��܂��A�Ƃ������Ƃ��Ȃ��悤�ɂ��Ă��������B
�{��͂܂��A���N�₩�ȉ�@�ɂ������߂�����A�Z���Ԃł�������Ə������悤�Əł����肷��ƁA��ӂ̉��߂ɑz��ȏ�̑���Ȏ��Ԃ������Ă��܂��A�Ƃ������s�������˂Ȃ���肾�ƌ������Ƃ��ł��܂��B�������ŁA�����w�^�ł��A�������Ԃ��������Ă��A�������ԓ��ɍ��i���C���ɓ͂��_��������悢�A�Ƃ������������邱�Ƃ́A�����A�����A�Z�p�J���ҁE�����҂Ƃ��āA����ꂽ���ԓI�\�Z�I������ĉȊw�̑����Ŋ����ł���Ȃ��Ƃł��B
[6](��������)�@�{��́A�قځA1�������Ɠ��ρA�����䂾���ʼnł��Ă��܂��̂ŁA����ȎZ�I���g���悤�ȂƂ���͂���܂���B�ł͖�����Ƀ��l���E�X�̒藝���g���܂������A�g��Ȃ��Ă��\�ł��B�ő�l��2�����Ȃ̂Ŋ�{�I�ƌ�����ł��傤�B���ʂȕ������Ă��Ȃ��������ł��R�c�R�c����Ă����ŏI�ɂ��ǂ�����Ƃ��ł���Ǝv���܂��B�ł����A(3)�܂Ő����ł������͋ɂ߂ď����ł͂Ȃ��ł��傤���B
���嗝�n�ł́A���̒����v�l���v���������́A���N�o�肳��Ă��܂����A�{��̂悤�ɁA��邱�Ƃ��͂����肵�Ă��āA��Ԃ̂����鏈�����������X�Ƒ����A�Ƃ����^�C�v�̖��͒������ƌ����܂��B�����Č����A�ʓ|�Ȍv�Z������������ς̖��͂��蓾�܂����A����͌v�Z�\�͂����悤�A�Ƃ������Ƃł��傤�B
�{��ɂ��ẮA��ԃx�N�g���̖��Ȃ̂Ŏd�����Ȃ��ƌ����ׂ����A���邢�́A�E�ϗ͂̂Ȃ��w���Ɍ����˂��o��҂��o����j��ς����̂��A�킩��܂��A���N�̓�����͑�ς��������낤�Ǝv���܂��B�{���(2)(3)�Ɏ��g��Ŗc��Ȏ��Ԃ��������̂ɂ�������炸�~�X�ɏI����������܂����݁A�������ƕ������đ��̖��Ɍ������������K�b�c�E�|�[�Y����A�Ƃ����\�}�́A�f���Ɏ��������̂ł͂Ȃ��C�����܂��B
���̍�����w�ł́A�ʓ|�ȏ��������Ȃ��鎝�v�͂����悤�A�Ƃ��������������܂����A���i�҂Ɉ�����\�͂�v�����Ă���̂��낤�ƍD�ӓI�Ɏ�邱�Ƃ��ł��܂��B�ł����A���嗝�n�ł́A���������H�v�����o����l���Ă��炦�Ȃ����̂��A�ƁA�����܂��B�����͈Ղ������͍���ł����A�����Ă��Ċy�����Ȃ�A����ł��ĉ��[���������āA���w�̎v�l�͂��v�������A�Ƃ����A�S���̎������嗝�n��ڎw���Ă݂悤�A�Ƃ����C�������������Ă����悤�ȁA'08�N�O��[5]�̂悤�Ȗ�肪���z�ł��B��Ԑ}�`�ł���A���X��x�̍������ł����A'96�N�O��[3]�A'90�N�O��[3]�̂悤�Ȗ����l�Ă��Ē����悤�Ɋ���Ă��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  ......[��]
......[��]