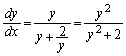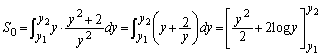���嗝�n���w'10�N�O��[4]
O�����_�Ƃ�����W���ʏ�̋Ȑ�
C�F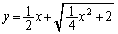
�ƁA���̏�̑��قȂ�2�_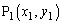 �C
�C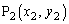 ���l����B
���l����B
(1) 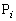 (
(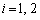 )��ʂ�x���ɕ��s�Ȓ����ƁA����
)��ʂ�x���ɕ��s�Ȓ����ƁA����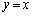 �Ƃ̌�_���A���ꂼ��
�Ƃ̌�_���A���ꂼ��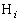 (
(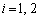 )�Ƃ���B���̂Ƃ�
)�Ƃ���B���̂Ƃ�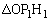 ��
��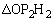 �̖ʐς͓��������Ƃ������B
�̖ʐς͓��������Ƃ������B (2) 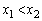 �Ƃ���B���̂Ƃ�C��
�Ƃ���B���̂Ƃ�C��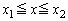 �͈̔͂ɂ��镔���ƁA����
�͈̔͂ɂ��镔���ƁA����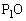 �C
�C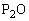 �Ƃň͂܂��}�`�̖ʐς��A
�Ƃň͂܂��}�`�̖ʐς��A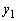 �C
�C ��p���ĕ\���B
��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�H�v�̕K�v�ȋ��ϖ��ł����A��蕶�̎w������������Ƃɂ��A�ʓ|�Ȍv�Z������ł��܂��B
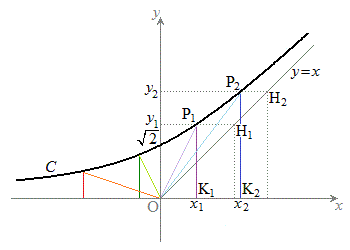 (1)
(1) 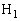 �C
�C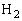 ��y���W��
��y���W��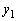 �C
�C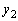 �ł����A����
�ł����A����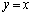 ��̓_�Ȃ̂ŁAx���W��y���W�Ɠ������A
��̓_�Ȃ̂ŁAx���W��y���W�Ɠ������A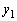 �C
�C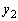 �ƂȂ�܂��B
�ƂȂ�܂��B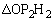 �C�܂�A���_O�C
�C�܂�A���_O�C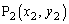 �C
�C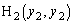 ��3���_�Ƃ���O�p�`�̖ʐ�
��3���_�Ƃ���O�p�`�̖ʐ�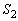 �́A
�́A�Ȑ�C��̓_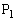 �C
�C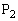 �̍��W���g���ĕ\����Ă���
�̍��W���g���ĕ\����Ă���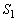 ��
��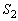 �������`�����Ă���̂ŁA�Ȑ�C��̓_
�������`�����Ă���̂ŁA�Ȑ�C��̓_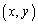 �ɂ��āA
�ɂ��āA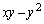 ���ǂ������l�ɂȂ邩�ׂĂ݂܂��B
���ǂ������l�ɂȂ邩�ׂĂ݂܂��B 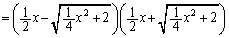
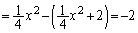 (���)�@����@
(���)�@����@�]���āA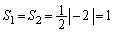
(2) ���߂�ʐς�S�C�Ȑ�C��x���A����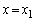 �C
�C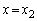 �ň͂ޖʐς�
�ň͂ޖʐς�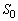 �C
�C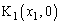 �C
�C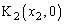 �Ƃ���
�Ƃ���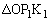 �̖ʐς�
�̖ʐς�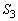 �C
�C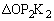 �̖ʐς�
�̖ʐς�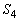 �Ƃ��āA
�Ƃ��āA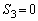 �C
�C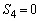 �ƂȂ�ꍇ���܂߂āA
�ƂȂ�ꍇ���܂߂āA (i) 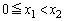 �̏ꍇ�A
�̏ꍇ�A (ii) 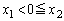 �̏ꍇ�A
�̏ꍇ�A (iii) 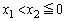 �̏ꍇ�A
�̏ꍇ�A ������̏ꍇ���A
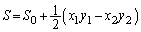 �@����A
�@����A��蕶�̗v���́u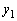 �C
�C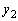 ��p���ĕ\���v�Ƃ������ƂȂ̂ŁA
��p���ĕ\���v�Ƃ������ƂȂ̂ŁA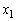 �C
�C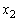 ���g�킸��
���g�킸��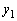 �C
�C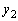 �ŕ\���悤�ɂ��܂��B�@��p����ƁA
�ŕ\���悤�ɂ��܂��B�@��p����ƁA 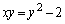 �@����B
�@����B����āA
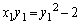 �C
�C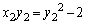
������A�́A
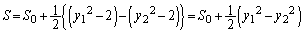 �@����C
�@����C�܂��A�Ȑ�C��̓_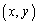 �ɂ����ẮA
�ɂ����ẮA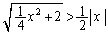 ���A
���A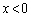 �̏ꍇ�ɂ��Ă��A
�̏ꍇ�ɂ��Ă��A ����āA�B���ӂ�y�Ŋ����āA
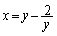 �@����D
�@����D���āA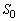 �ɂ��āA
�ɂ��āA ������A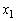 �C
�C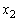 ���g�킸
���g�킸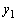 �C
�C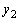 �ŕ\���悤�ɂ��邽�߂ɁA
�ŕ\���悤�ɂ��邽�߂ɁA 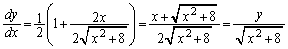 �@����F
�@����F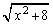 ������܂����A�D��p���āA
������܂����A�D��p���āA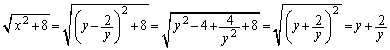 �@(��
�@(�� 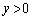 )
)�F�ɑ�����āA
����āA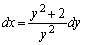 x�F
x�F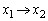 �̂Ƃ�y�F
�̂Ƃ�y�F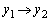
�������āA�E�́A �C�ɑ������ƁA
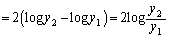 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 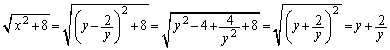 �@(��
�@(��