���嗝�n���w '10 �N�O�� [6] �l�ʑ� OABC �ɂ����āA 4 �̖ʂ͂��ׂč����ł���A 3 �_ O �C A �C B ���܂ޕ��ʂ� L �Ƃ���B (1) �_ C ���畽�� L �ɂ��낵�������̑��� H �Ƃ����B (2) ���݂������� t �ɑ��āA���� OA �C OB �e�X�� t �F 2 �_ L �ɐ����ȕ��ʂ� M �Ƃ���Ƃ��A���� M �ɂ��l�ʑ� OABC �̐���̖ʐ� (3) t �� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� �@��ԓI�Ȕ��z�͂Ƃ��v�l�͂Ƃ��������A�ʓ|�Ȍv�Z�����������ԃx�N�g���̖��ł��B�̗͔h�̏����ȊO�́A��{���� (1) �͂Ƃ������A����I�ɂ͌�ɂ���̂�����낤�Ǝv���܂��B (1) 4 �̖ʂ������A�Ƃ������ƂŁA�E�}�̂悤�ɁA
�� �� �� �́� OAB ���܂ޕ��� L ��̓_�Ȃ̂ŁA α �C β �������Ƃ��āA CH �͕��� L �ɐ����Ȃ̂ŁA �@����@ �@����A �@�C�A��A�����āA
�C �� �� ] (2) �C K �Ƃ��� ( �������� ���Q�� ) �A �@����B H ������ t �C p �̒l�ׂ܂��B (1) �̌��ʂƇB�̌W�����r���āA �B���A
�@����C �Ə�����̂ŁA P �C�_ Q �Ƃ���ƁA H �͐��� PQ ��̓_�ɂȂ��Ă��܂��B�܂��A�_ H ��ʂ蕽�� L �ɐ����ȕ��ʂ́� CPQ ���܂ޕ��ʂł���A 2 �_ L �ɐ����ȕ��� M �́A ( �� CPQ ���܂ޕ��ʂł��邱�Ƃ��܂߂� ) �� CPQ �ɕ��s�ł��B����Ɍ����A�� CPQ �� P �C Q ��ʂ镽�� M �ɂ��l�ʑ̂̐���Ȃ̂ŁA�� CPQ �̖ʐς́A M �ɂ��l�ʑ� OABC �̐���̖ʐς����߂邽�߂ɂ́A�� CPQ �̖ʐς����߁A��������l���邱�ƂɂȂ�܂��B CPQ �ƕ��s�ŕ� AB ��ʂ镽�� ( �]���ĕ��� L �ɐ��� ) �ƒ��� OC �Ƃ̌�_�� D �Ƃ���ƁA�� CPQ �Ɓ� DAB �͑����ŁA PQ �F AB = OP �F OA = �F 1 ���A�� CPQ �̖ʐ� DAB �̖ʐ� ( �ʐϔ�E�̐ϔ� ���Q�� ) �A �� DAB �̖ʐς����߂邽�߂ɁA OP �F OA = OQ �F OB = OC �F OD = �F 1 ���A �� �� �D���A�� CPQ �̖ʐ� (i) �C OP ��A���� OQ ��ɂ���Ƃ� ( �[�_ O ������ ) �A�܂�A �� �@����E ���D��L�ŁA���� OH �ƒ��� BA �Ƃ̌�_�� E �Ƃ��āA�C���A
�Ƃ킩��̂ŁA
�� �Ƃ��邱�Ƃ��ł��܂��B
(ii) �C PA ��A���� QB ��ɂ���Ƃ� ( ���[������ ) �A�܂�A M �ƒ��� OC �C���� BC �C���� AC �Ƃ̌�_�� M �ɂ��l�ʑ� OABC �̐���́A�� OB �F = 1 �F OD = t �F 1 �C OC = �F �� ������A�� �� �ȏ�܂Ƃ߂āA ......[ �� ] �ɂ����āA �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@ ���嗝�n���w TOP �@�@ ���w TOP �@�@ TOP �y�[�W�ɖ߂� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B �e���̒��쌠�� © 2005-2024 (�L)����� ��w�y�w�m ���������t���I ���n��w�l�b�g�m ��w�y�w�m (���ē��������� )������́A������܂Ń��[�� �� 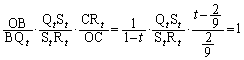
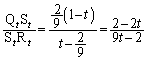
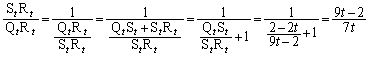
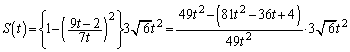
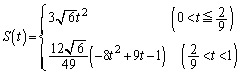 ......[��]
......[��]