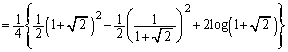���嗝�H���w'10�N[4]
xyz��Ԃɂ����āA2�_P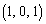 �CQ
�CQ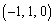 ���l����B����PQ��x���̎����1��]���ē�����Ȗʂ�S�Ƃ���B�ȉ��̖₢�ɓ�����B
���l����B����PQ��x���̎����1��]���ē�����Ȗʂ�S�Ƃ���B�ȉ��̖₢�ɓ�����B
(1) �Ȗ�S�ƁA2�̕���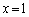 �����
�����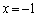 �ň͂܂�闧�̂̑̐ς����߂�B
�ň͂܂�闧�̂̑̐ς����߂�B (2) (1)�̗��̂̕���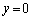 �ɂ�������A����
�ɂ�������A����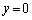 ��ɂ����Đ}������B
��ɂ����Đ}������B (3) ��ϕ�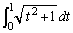 �̒l��
�̒l��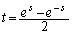 �ƒu�����邱�Ƃɂ���ċ��߂�B�����p���āA(2)�̐���̖ʐς����߂�B
�ƒu�����邱�Ƃɂ���ċ��߂�B�����p���āA(2)�̐���̖ʐς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@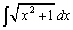 �Ƃ�����ϕ��́A����A�c��̓����ł悭�������܂��B
�Ƃ�����ϕ��́A����A�c��̓����ł悭�������܂��B
I���ڍ�����2�Ŋ���ƁA
�J�b�R���̐ϕ��́A
�𗘗p���āA
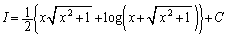 (C�F�ϕ��萔)
(C�F�ϕ��萔)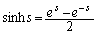 ���g���Ēu���ϕ�����Z�I���g���悤�Ɏw�肳��Ă��܂��B�Ȃ��A�u���ϕ�(����3)���Q�Ƃ��Ă��������B
���g���Ēu���ϕ�����Z�I���g���悤�Ɏw�肳��Ă��܂��B�Ȃ��A�u���ϕ�(����3)���Q�Ƃ��Ă��������B
(1) 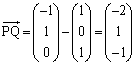
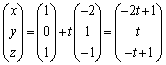 �@(����PQ��̓_�ł�
�@(����PQ��̓_�ł�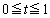 )
)����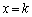 �ƒ���PQ�̌�_R�́A
�ƒ���PQ�̌�_R�́A �� 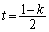
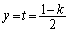 �C
�C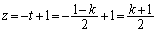
�_R��x���̎����1��]���Ăł���~�̔��a�͓_R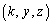 ��x���Ƃ̋����A�����A�_
��x���Ƃ̋����A�����A�_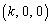 �Ƃ̋����ɓ������A����2��́A
�Ƃ̋����ɓ������A����2��́A 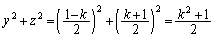 �@����@
�@����@���̉~�́A�Ȗ�S��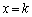 �Ő����Ƃ��ɂł���~�ł��B�~�̖ʐ�
�Ő����Ƃ��ɂł���~�ł��B�~�̖ʐ�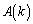 �́A
�́A �_R������PQ��ɂ���Ƃ��́A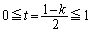 ���Ax���Wk�́A
���Ax���Wk�́A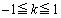 �ƂȂ�܂��B
�ƂȂ�܂��B
�Ȗ�S�ƁA2�̕���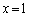 �����
�����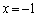 �ň͂܂������K�̑̐�V�́A
�ň͂܂������K�̑̐�V�́A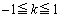 ���A
���A 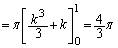 ......[��]
......[��]
(2) (1)�̗���K���̓_��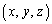 �Ƃ���ƁA����K��
�Ƃ���ƁA����K��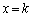 (
(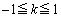 )�Ő����Ƃ��ɂł���f�ʂ̉~���̓_
)�Ő����Ƃ��ɂł���f�ʂ̉~���̓_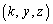 �́A(1)�ɏo�Ă����A
�́A(1)�ɏo�Ă����A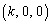 �𒆐S�Ƃ����a��2����@�Ƃ���~���̓����ƂȂ�̂ŁA�@���A
�𒆐S�Ƃ����a��2����@�Ƃ���~���̓����ƂȂ�̂ŁA�@���A 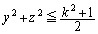 (
(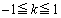 )
)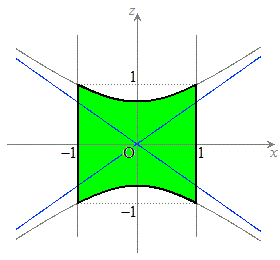 �����܂��B�����ŁAx���Wk��x�ɏ��������A
�����܂��B�����ŁAx���Wk��x�ɏ��������A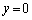 �Ƃ���ƁA����K�̕���
�Ƃ���ƁA����K�̕���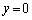 �ɂ�������̓_
�ɂ�������̓_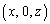 �́A
�́A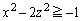 (
(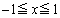 )
)�����܂��B���E��(�E�}����)�́A
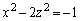 �@����A
�@����A�ƁA����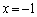 �C����
�C����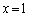 �ł����C�A�́A
�ł����C�A�́A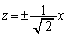 ��Q�ߐ�(�E�}��)�Ƃ����o�Ȑ��ł��B
��Q�ߐ�(�E�}��)�Ƃ����o�Ȑ��ł��B
������A�����}������ƁA�E�}���ΐF���F����(���E�����܂�)�B
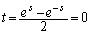 �Ƃ���ƁA
�Ƃ���ƁA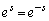 �C
�C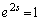 �C
�C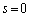
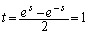 �Ƃ���ƁA
�Ƃ���ƁA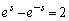 �C
�C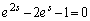 �C
�C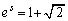 (
(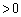 )�C
)�C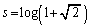
����āAt�F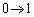 �̂Ƃ��As�F
�̂Ƃ��As�F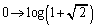
�A���A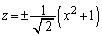 (2)�̐}�������z���Cx���Ɋւ��đΏ̂ŁA����̖ʐς́A�o�Ȑ��ƒ���
(2)�̐}�������z���Cx���Ɋւ��đΏ̂ŁA����̖ʐς́A�o�Ȑ��ƒ���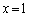 �Cx���Az���ň͂܂�镔���̖ʐς�4�{�ɓ������A
�Cx���Az���ň͂܂�镔���̖ʐς�4�{�ɓ������A 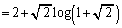 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 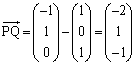
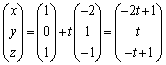 �@(����PQ��̓_�ł�
�@(����PQ��̓_�ł�