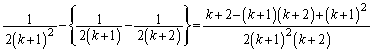���嗝�n���w'10�N�O��[2]
(1) ���ׂĂ̎��R��k�ɑ��āA���̕s�����������B
(2) 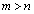 �ł���悤�Ȃ��ׂĂ̎��R��m��n�ɑ��āA���̕s�����������B
�ł���悤�Ȃ��ׂĂ̎��R��m��n�ɑ��āA���̕s�����������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��ϕ��Ɋւ���s���������ł��B�����|�̉ߋ���07�N�O��[6]�Ɣ�ׂ�ƁA�f���ɍl���čs���镪�����A�{��̕������e�Ղ����m��܂���B
 (1) ��ϕ��̔�ϕ����́A
(1) ��ϕ��̔�ϕ����́A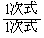 �̌`�̕������ł��B�����
�̌`�̕������ł��B������@�́A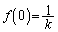 �C
�C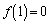 ���A�Ȑ�
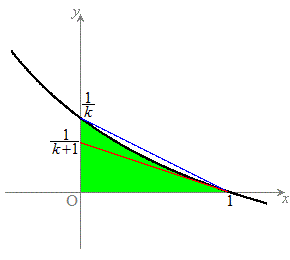
���A�Ȑ�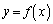 ��x���Cy���Ƃň͂ޕ����A�����A�E�}���ΐF���F�������ʐ��ŁA
��x���Cy���Ƃň͂ޕ����A�����A�E�}���ΐF���F�������ʐ��ŁA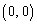 �C
�C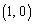 �C
�C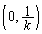 ��3���_�Ƃ���O�p�`�̖ʐ�
��3���_�Ƃ���O�p�`�̖ʐ�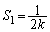 �����������Ȃ�̂ŁA���̂��Ƃ���^�s�����̉E���̕s���������������ł��B
�����������Ȃ�̂ŁA���̂��Ƃ���^�s�����̉E���̕s���������������ł��B
���l�ɍl���āA�^�s�����̍����̕s�����́A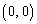 �C
�C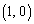 �C
�C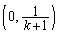 ��3���_�Ƃ���O�p�`�̖ʐ�
��3���_�Ƃ���O�p�`�̖ʐ�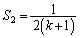 �Ɣ�r���邱�Ƃɂ�莦����̂ł͂Ȃ����A�ƁA���҂ł��܂��B
�Ɣ�r���邱�Ƃɂ�莦����̂ł͂Ȃ����A�ƁA���҂ł��܂��B
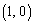 �C
�C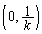 ��ʂ������́A
��ʂ������́A 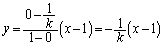 �@����A
�@����A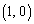 �C
�C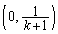 ��ʂ钼���́A
��ʂ钼���́A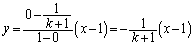 �@����B
�@����B�A��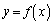 �́A
�́A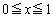 �ɂ����āA
�ɂ����āA ���A�����A�͋Ȑ�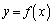 ����㑤�ɂ���A
����㑤�ɂ���A
�B��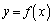 �́A
�́A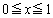 �ɂ����āA
�ɂ����āA ���A�����B�͋Ȑ�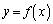 ���牺���ɂ���܂��B
���牺���ɂ���܂��B
������A�����B�C�Ȑ�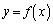 �C�����A��x���Cy���Ƃň͂ޖʐς��r���āA
�C�����A��x���Cy���Ƃň͂ޖʐς��r���āA �� 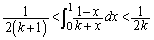
(2) �����ׂ��s�����̉E�ӂ́A
�ƂȂ��Ă��āA���l�ɁA�s�����̍��ӂɂ��Ă��A
�ł��邱�Ƃɒ��ڂ��܂��B
��ϕ�I���v�Z�������ʂ���ꂽ(1)�̕s����
�̊e�ӂ�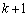 �Ŋ����Ăł���s����
�Ŋ����Ăł���s���� 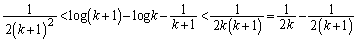 �@����C
�@����C�̉E�ӂ��A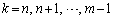 �Ƃ��ĉ������킹��ƁA
�Ƃ��ĉ������킹��ƁA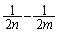 �ɂȂ�̂ŁA(1)�̌��ʂ�ό`���ĉ������킹��悢(����̋��a�Z�@���Q��)�A�Ƃ������ƂɂȂ�܂��B���ӂ̌`���E�ӂɍ��킹�āA
�ɂȂ�̂ŁA(1)�̌��ʂ�ό`���ĉ������킹��悢(����̋��a�Z�@���Q��)�A�Ƃ������ƂɂȂ�܂��B���ӂ̌`���E�ӂɍ��킹�āA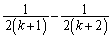 �ɂȂ��Ă���Ɠs�����悢�̂ł����A
�ɂȂ��Ă���Ɠs�����悢�̂ł����A ���A
�ƂȂ�̂ŁA�C���A
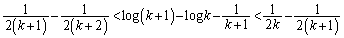 �@����D
�@����D�D�ɂ����āA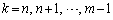 �Ƃ��āA
�Ƃ��āA ������
�ӁX�������킹�邱�Ƃɂ��A
�� 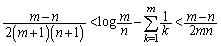
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B