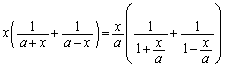東大理系数学'07年前期[6]
以下の問いに答えよ。
(1) 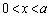 をみたす実数x,aに対し、次を示せ。
をみたす実数x,aに対し、次を示せ。 (2) (1)を利用して、次を示せ。
ただし、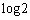 は2の自然対数を表す。
は2の自然対数を表す。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 何でもないように見えるこういう問題が意外と手強かったりします。(2)は、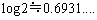 なのですが、示すべき式の範囲が狭いので、うまく行かなければ、後回しにするべきです。ここでは、試験場でハマってしまい、試行錯誤している状況を想定してやってみます。
なのですが、示すべき式の範囲が狭いので、うまく行かなければ、後回しにするべきです。ここでは、試験場でハマってしまい、試行錯誤している状況を想定してやってみます。
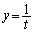 は、
は、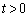 の範囲において、減少関数であり、そのグラフは下に凸です。
の範囲において、減少関数であり、そのグラフは下に凸です。
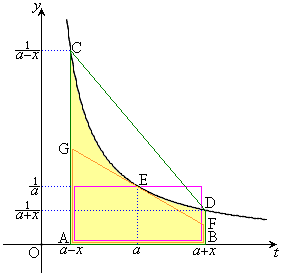
従って、曲線: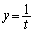 は、曲線上の2点C,Dを結ぶ線分から下側に来ます。
は、曲線上の2点C,Dを結ぶ線分から下側に来ます。
よって、曲線とt軸,直線: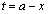 ,直線:
,直線: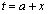 で囲まれる部分(右図で黄色の部分)の面積
で囲まれる部分(右図で黄色の部分)の面積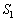 は、台形ACDB(右図緑線で囲まれた部分)の面積
は、台形ACDB(右図緑線で囲まれた部分)の面積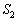 よりも小さくなります(定積分と面積を参照)。
よりも小さくなります(定積分と面積を参照)。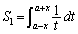 ,
,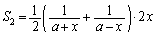
より、
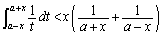 ・・・①
・・・①ここで、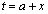 とすると、
とすると、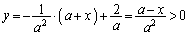 (
(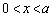 )これより、この接線と直線:
)これより、この接線と直線: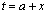 は、第1象限において交点Fをもちます。
は、第1象限において交点Fをもちます。
接線と直線: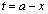 との交点をGとすると、接線は、曲線:
との交点をGとすると、接線は、曲線: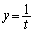 から下側に来るので、台形AGFB(右図橙色の線で囲まれた部分)の面積
から下側に来るので、台形AGFB(右図橙色の線で囲まれた部分)の面積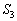 は、
は、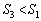
ところで、Eは線分FGの中点なので、台形AGFBの面積は、Eを通りx軸に平行な直線、x軸、直線: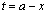 ,直線:
,直線: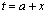 で囲まれる部分(右図ピンクの長方形で囲まれた部分)の面積
で囲まれる部分(右図ピンクの長方形で囲まれた部分)の面積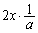 に等しく、
に等しく、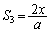
∴ 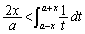 ・・・②
・・・② ①,②より示せました。別解 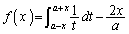 とおくと、
とおくと、 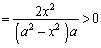 (
(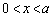 )
)よって、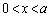 において、
において、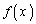 は増加。
は増加。 ∴ 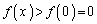 ∴
∴ 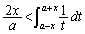
また、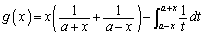 とおくと、
とおくと、 よって、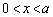 において、
において、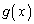 は増加。
は増加。 ∴ 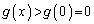 ∴
∴ 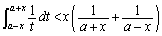
(2) 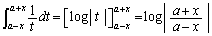 と(1)より、
と(1)より、 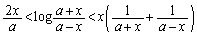 ・・・③
・・・③目標は、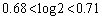 ・・・④ ですが、
・・・④ ですが、
③において、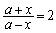 としてみると、
としてみると、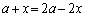 ,
,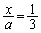
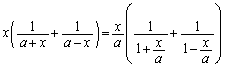 ・・・⑤
・・・⑤これでは、③は、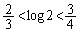 となり、④を示すことができません。
となり、④を示すことができません。
④を示すためには、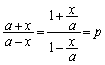 (
(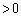 )としたときに、
)としたときに、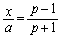 より、
より、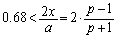 かつ
かつ 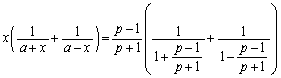 (∵ ⑤)
(∵ ⑤)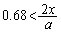 かつ
かつ 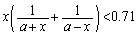
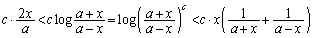 ・・・⑦
・・・⑦となりますが、このときには、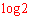 をひねり出すために、
をひねり出すために、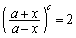 ,つまり、
,つまり、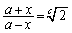 とおくことになるでしょう。
とおくことになるでしょう。
面倒なので、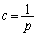 (
(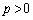 )として、
)として、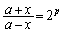 とおくことにします。
とおくことにします。 ⑦の左の不等号は、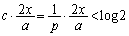 より、
より、 となって欲しいわけですが、整理すると、
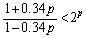 ,ただし、
,ただし、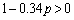
この不等式は、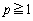 では、
では、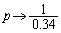 のとき、左辺が急激に無限大に近づくので成り立ちません。
のとき、左辺が急激に無限大に近づくので成り立ちません。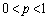 の範囲でもきわどい不等式ですが、
の範囲でもきわどい不等式ですが、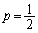 としてみると、
としてみると、 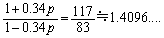 ,
,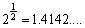
となって、不等式が成立します。
これで、③の各辺に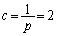 をかけた不等式において、
をかけた不等式において、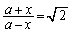 を代入、つまり、
を代入、つまり、 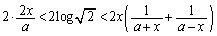 ,
,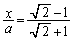
とすれば、④が示せそうだ、ということになります。
ですが、試験場でこんなことをやっていたら、合格はとても無理です。この問題は、最初から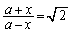 とおくことに気づくのでなければ、試験場では断念が賢明です。
とおくことに気づくのでなければ、試験場では断念が賢明です。
解答は、以下のようになるでしょう。
③において、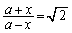 とおくと、
とおくと、 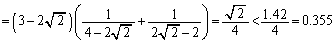 (
(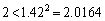 です)
です)∴ 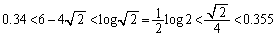 各辺に2をかけて、
各辺に2をかけて、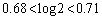
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 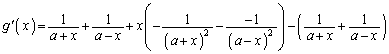
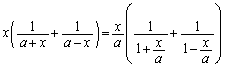 ・・・⑤
・・・⑤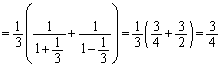
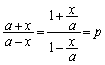 (
(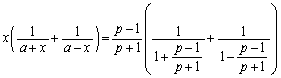 (∵ ⑤)
(∵ ⑤)