���嗝�n���w'10�N�O��[3]
2�̔�L��R�C�{�[��30�A�R�C�������ŕ\�Ɨ������m�� �ŏo��R�C��1����p�ӂ���Bx��0�ȏ�30�ȉ��̐����Ƃ���BL��x�CR��
�ŏo��R�C��1����p�ӂ���Bx��0�ȏ�30�ȉ��̐����Ƃ���BL��x�CR�� �̃{�[�������A���̑���(��)���J��Ԃ��B
�̃{�[�������A���̑���(��)���J��Ԃ��B
(��) ��L�ɓ����Ă���{�[���̌���z�Ƃ���B�R�C���𓊂��A�\���o��Δ�R���甠L�ɁA�����o��Δ�L���甠R�ɁA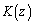 �̃{�[�����ڂ��B�������A
�̃{�[�����ڂ��B�������A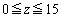 �̂Ƃ�
�̂Ƃ� �C
�C �̂Ƃ�
�̂Ƃ�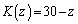 �Ƃ���B
�Ƃ���B
m��̑���̌�A��L�̃{�[���̌���30�ł���m����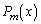 �Ƃ���B���Ƃ���
�Ƃ���B���Ƃ��� �ƂȂ�B�ȉ��̖�(1)�C(2)�C(3)�ɓ�����B
�ƂȂ�B�ȉ��̖�(1)�C(2)�C(3)�ɓ�����B
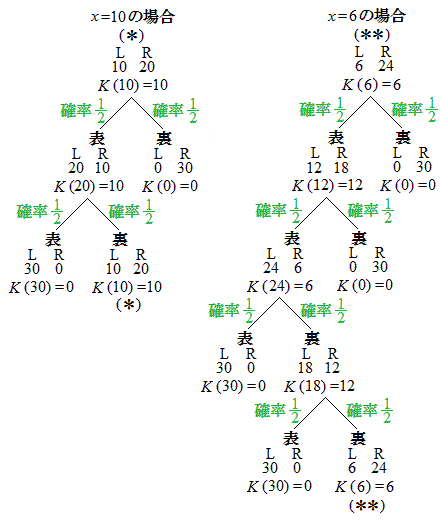
(1) 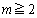 �̂Ƃ��Ax�ɑ��Ă��܂�y��I�сA
�̂Ƃ��Ax�ɑ��Ă��܂�y��I�сA ��
�� �ŕ\���B
�ŕ\���B (2) n�����R���Ƃ���Ƃ��A �����߂�B
�����߂�B (3) n�����R���Ƃ���Ƃ��A �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���̖���[1]�Ɠ��l�ɁA����ł͂��Ȃ�ȑO�ɂ悭�o�肳��Ă����^�C�v�̖��ł�(�Ⴆ��90�N�O��[6]�A84�N[5])�B(1)�̏o��Ӑ}�����݂ɂ����̂ł����A�Q�����𗧂Ăċ@�B�I�ɏ�������A�Ƃ����q���g�ł��B��ʓI��x�ōl���悤�Ƃ���Ɠ������ɂ����˂܂��A(1)���ł��Ȃ��Ă��A(2)�C(3)�́A �̏ꍇ��
�̏ꍇ�� �̏ꍇ�����Ȃ̂ŁA���`�}�������čs���A(1)�𗘗p���Ȃ��Ă��ł��܂��B
�̏ꍇ�����Ȃ̂ŁA���`�}�������čs���A(1)�𗘗p���Ȃ��Ă��ł��܂��B
(1) ����(��)����ʓI��x�ōl���čs���ƁA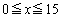 ��
��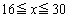 �̏ꍇ�������l���ɂ���(���������������ē��H��81�N[1]�ȂǂɌ���ꂽ���̂ł�)�A�������Ղ��̂ŁA������ł́A�ŏ�����
�̏ꍇ�������l���ɂ���(���������������ē��H��81�N[1]�ȂǂɌ���ꂽ���̂ł�)�A�������Ղ��̂ŁA������ł́A�ŏ�����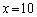 �C
�C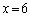 �̏ꍇ�Ŏ��`�}�������čs���̂��悢�Ǝv���܂��B�E�}��
�̏ꍇ�Ŏ��`�}�������čs���̂��悢�Ǝv���܂��B�E�}�� �̏ꍇ��
�̏ꍇ��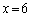 �̏ꍇ�ɂ��Ď��`�}�������܂��B
�̏ꍇ�ɂ��Ď��`�}�������܂��B  �̏ꍇ�A����(��)��1��s���ƁA�����o���Ƃ��ɁAL��0�CR��30�Ƃ�����ԂɂȂ�܂����A���̌��
�̏ꍇ�A����(��)��1��s���ƁA�����o���Ƃ��ɁAL��0�CR��30�Ƃ�����ԂɂȂ�܂����A���̌��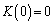 �ƂȂ�{�[�����ڂ�����͍s��ꂸ�A���̂܂ܕω����Ȃ��Ȃ�܂��B�܂��A����(��)��1��s���������ł́AL��30�Ƃ�����Ԃɂ͂Ȃ蓾�Ȃ��̂ŁA
�ƂȂ�{�[�����ڂ�����͍s��ꂸ�A���̂܂ܕω����Ȃ��Ȃ�܂��B�܂��A����(��)��1��s���������ł́AL��30�Ƃ�����Ԃɂ͂Ȃ蓾�Ȃ��̂ŁA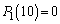 �ł��B����(��)��2��s���ƁA�m��
�ł��B����(��)��2��s���ƁA�m�� �Ŕ�L�̌���30�ɂȂ�܂��B����āA
�Ŕ�L�̌���30�ɂȂ�܂��B����āA �@����@
�@����@�ł��B����ȍ~ �ƂȂ�A���̂܂ܔ��̃{�[���̌��͕ω����Ȃ��Ȃ�܂��B�܂��A�m��
�ƂȂ�A���̂܂ܔ��̃{�[���̌��͕ω����Ȃ��Ȃ�܂��B�܂��A�m��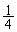 ��L��10�Ƃ�����ԂɂȂ�̂ł����A����͍ŏ��̏��(��)�Ɠ�����Ԃł��B�ʉ��ɂ��̂��Ƃɒ��ڂ�������q���܂��B
��L��10�Ƃ�����ԂɂȂ�̂ł����A����͍ŏ��̏��(��)�Ɠ�����Ԃł��B�ʉ��ɂ��̂��Ƃɒ��ڂ�������q���܂��B
 �̏ꍇ�ɂ́A����(��)��1��A�܂��́A2��s���Ƃ��ɂ́AL��30�Ƃ�����Ԃɂ͂Ȃ蓾�Ȃ��̂ŁA
�̏ꍇ�ɂ́A����(��)��1��A�܂��́A2��s���Ƃ��ɂ́AL��30�Ƃ�����Ԃɂ͂Ȃ蓾�Ȃ��̂ŁA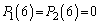 �ł��B3��s���ƁA�m��
�ł��B3��s���ƁA�m��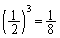 �Ŕ�L�̌���30�ɂȂ�̂�
�Ŕ�L�̌���30�ɂȂ�̂�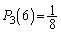 �C����ȍ~
�C����ȍ~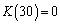 �ƂȂ�A���̂܂ܔ��̃{�[���̌��͕ω����Ȃ��Ȃ�܂��B4��s���ƁA
�ƂȂ�A���̂܂ܔ��̃{�[���̌��͕ω����Ȃ��Ȃ�܂��B4��s���ƁA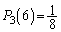 �ƂȂ�ꍇ�ȊO�ɂ���Ɋm��
�ƂȂ�ꍇ�ȊO�ɂ���Ɋm��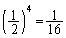 �Ŕ�L�̌���30�ɂȂ�A
�Ŕ�L�̌���30�ɂȂ�A  �@����A
�@����A�Ƃ�����ɂ��āA�W������邱�Ƃ��ł��܂��B
�A���A������ł������蔲�����Ȃ��ꍇ�A(2)�C(3)�͕ʉ��̂悤�ɍl���ĉ��Ă��������B
�ȏ�܂��āA �̂Ƃ��ŏ���L�̌���x��m����L�̌���30�ɂȂ�m��
�̂Ƃ��ŏ���L�̌���x��m����L�̌���30�ɂȂ�m�� �ƁA�ŏ���1��̑�����L�̌���y�ŁA�ȍ~
�ƁA�ŏ���1��̑�����L�̌���y�ŁA�ȍ~ ����L�̌���30�ɂȂ�m��
����L�̌���30�ɂȂ�m��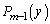 �Ƃ̊W�����߂܂��B
�Ƃ̊W�����߂܂��B
�����ŁA�܂����ӂ��Ȃ�������Ȃ��̂́A����(��)�ɂ�����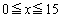 �̂Ƃ���
�̂Ƃ���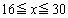 �̂Ƃ��Ƃňړ���������قȂ�Ƃ������Ƃł��B�ꍇ�������K�v�ɂȂ�܂��B
�̂Ƃ��Ƃňړ���������قȂ�Ƃ������Ƃł��B�ꍇ�������K�v�ɂȂ�܂��B (i) 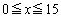 �̂Ƃ��A
�̂Ƃ��A ���A�\���o���(�m��
���A�\���o���(�m��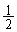 )L��
)L��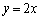 �ƂȂ�A�ȍ~
�ƂȂ�A�ȍ~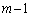 ��̑����L��30�ɂȂ�m����
��̑����L��30�ɂȂ�m����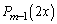 �C�����o���(�m��
�C�����o���(�m�� )L��
)L�� �ƂȂ�A�ȍ~
�ƂȂ�A�ȍ~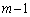 ��̑����L��30�ɂȂ�m����
��̑����L��30�ɂȂ�m���� �ɂȂ�܂��B�]���āA
�ɂȂ�܂��B�]���āA  �@����B
�@����B(ii) 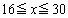 �̂Ƃ��A
�̂Ƃ��A ���A�\���o���(�m��
���A�\���o���(�m�� )L��
)L�� �ƂȂ�A�ȍ~
�ƂȂ�A�ȍ~ ��̑����L��30�ɂȂ�m����
��̑����L��30�ɂȂ�m����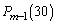 �C�����o���(�m��
�C�����o���(�m��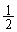 )L��
)L�� �ƂȂ�A�ȍ~
�ƂȂ�A�ȍ~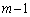 ��̑����L��30�ɂȂ�m����
��̑����L��30�ɂȂ�m����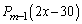 �ɂȂ�܂��B�]���āA
�ɂȂ�܂��B�]���āA 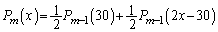 �@����C
�@����C�O�q�����悤�ɁAL�̌���0�ɂȂ邩30�ɂȂ��Ă��܂��ƁA �ƂȂ�A�ړ�����{�[���̌���0�ŁA����ȍ~�AL�̌��͕ω����Ȃ��Ȃ�܂��B�܂�AL�̌���0�ɂȂ��Ă��܂��ƁA�ȍ~���삵�Ă��AL�̌���30�ɂȂ蓾�܂���B����āA�B��
�ƂȂ�A�ړ�����{�[���̌���0�ŁA����ȍ~�AL�̌��͕ω����Ȃ��Ȃ�܂��B�܂�AL�̌���0�ɂȂ��Ă��܂��ƁA�ȍ~���삵�Ă��AL�̌���30�ɂȂ蓾�܂���B����āA�B�� ��0�ł��B�܂��AL�̌���30�ɂȂ��Ă��܂��ƁA�ȍ~���삵�Ă��AL�̌��͂�����30�ł��B����āA�C��
��0�ł��B�܂��AL�̌���30�ɂȂ��Ă��܂��ƁA�ȍ~���삵�Ă��AL�̌��͂�����30�ł��B����āA�C��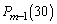 ��1�ł��B
��1�ł��B
����āA �̂Ƃ��A
�̂Ƃ��A 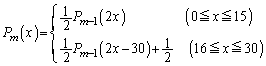 ......[��]
......[��]
(2) �ȉ��ł́A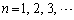 �Ƃ��܂��B(1)�̌��ʂ�p���āA
�Ƃ��܂��B(1)�̌��ʂ�p���āA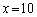 �̂Ƃ��A
�̂Ƃ��A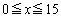 ���A
���A �������A
 �@����D
�@����D
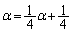 �@����E
�@����E��  �D�|�E���A
�D�|�E���A ���� �́A����
�́A����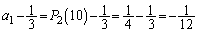 (�� �@)�C����
(�� �@)�C���� �����䐔���ŁA
�����䐔���ŁA ��  ......[��]
......[��]
(3) (1)�̌��ʂ�p���āA
�����ŁA �Ƃ����ƁA
�Ƃ����ƁA  �@����F
�@����F
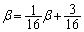 �@����G
�@����G�� 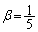 �F�|�G���A
�F�|�G���A ����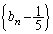 �́A����
�́A���� (�� �A)�C����
(�� �A)�C����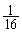 �̓��䐔��ŁA
�̓��䐔��ŁA �� 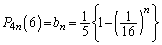 ......[��]
......[��]
�ʉ��D(1)���蔲�����Ȃ��Ă����߂邱�Ƃ͂���܂���B���`�}�ŁA���̑���̌�ɁA�ŏ��̏��(��)���o�Ă��邱�Ƃ𗘗p�����(2)�C(3)���ł��܂��B�ŏ�����(1)��������āA�ȉ��̂悤�ɂ���������_�I�ɂ͂悢�����m��܂���B
(2)  �̂Ƃ��A2��̑����Ɋm��
�̂Ƃ��A2��̑����Ɋm��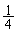 �ōŏ��̏��(��)���o�Ă��܂��B
�ōŏ��̏��(��)���o�Ă��܂��B �ŏ�����n�߂�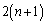 ��̑�����L�̌���30�ɂȂ�m����
��̑�����L�̌���30�ɂȂ�m���� �ł��B2����(��)����n�߂�
�ł��B2����(��)����n�߂�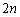 ��̑�����L�̌���30�ɂȂ�m����
��̑�����L�̌���30�ɂȂ�m����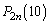 �ł��B
�ł��B
���`�}���A�ŏ�����n�߂�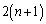 ��̑�����L�̌���30�ɂȂ�̂́A�ŏ���2��ŁA2���ĕ\���o���ꍇ(�m��
��̑�����L�̌���30�ɂȂ�̂́A�ŏ���2��ŁA2���ĕ\���o���ꍇ(�m��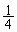 )�ƁA2��̑���ŕ\�A���Əo��(�m��
)�ƁA2��̑���ŕ\�A���Əo��(�m�� )����Ɉȍ~��
)����Ɉȍ~��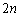 ��̑����L�̌���30�ɂȂ�ꍇ�ł��B�܂�A
��̑����L�̌���30�ɂȂ�ꍇ�ł��B�܂�A ���̌�A2���ԑQ�����������̂͏�L�̒ʂ�ł��B
(3) 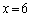 �̂Ƃ��A4��̑����Ɋm��
�̂Ƃ��A4��̑����Ɋm�� �ōŏ��̏��(����)���o�Ă��܂��B
�ōŏ��̏��(����)���o�Ă��܂��B �ŏ�����n�߂�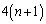 ��̑�����L�̌���30�ɂȂ�m����
��̑�����L�̌���30�ɂȂ�m����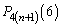 �ł����A�����Ȃ�̂́A�ŏ���4��ŁA3���ĕ\���o���ꍇ(�m��
�ł����A�����Ȃ�̂́A�ŏ���4��ŁA3���ĕ\���o���ꍇ(�m�� )�ƁA4��̑���ŕ\�A�\�A���A�\�Əo���ꍇ(�m��
)�ƁA4��̑���ŕ\�A�\�A���A�\�Əo���ꍇ(�m��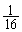 )�ƁA�\�A�\�A���A���Əo��(�m��
)�ƁA�\�A�\�A���A���Əo��(�m��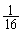 )����Ɉȍ~��
)����Ɉȍ~��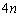 ��̑����L�̌���30�ɂȂ�ꍇ(�m��
��̑����L�̌���30�ɂȂ�ꍇ(�m�� )�ł��B�܂�A
)�ł��B�܂�A ���̌�A2���ԑQ�����������̂͏�L�̒ʂ�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 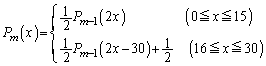 ......[��]
......[��]