���嗝�n���w'10�N�O��[5]
C�a1�̉~���Ƃ��AA��C���1�_�Ƃ���B3�_P�CQ�CR��A������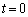 �ɏo�����AC����e�X���̑����ŁAP�CQ�͔����v���ɁAR�͎��v���ɁA����
�ɏo�����AC����e�X���̑����ŁAP�CQ�͔����v���ɁAR�͎��v���ɁA����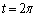 �܂œ����BP�CQ�CR�̑����́A���ꂼ��m�C1�C2�ł���Ƃ���B(���������āAQ��C�����傤�Lj������B)�������Am��
�܂œ����BP�CQ�CR�̑����́A���ꂼ��m�C1�C2�ł���Ƃ���B(���������āAQ��C�����傤�Lj������B)�������Am��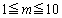 ���݂��������ł���B��PQR��PR���ΕӂƂ��钼�p�ӎO�p�`�ƂȂ�悤�ȑ���m�Ǝ���t�̑g�����ׂċ��߂�B
���݂��������ł���B��PQR��PR���ΕӂƂ��钼�p�ӎO�p�`�ƂȂ�悤�ȑ���m�Ǝ���t�̑g�����ׂċ��߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��]�^���̖��̂悤�Ɍ����܂����A�����I�ɂ���������ł��B��������`�F�b�N����͈͂��i�邱�Ƃ��ڕW�ł��B�ȉ��ł́At�̉\����6�ʂ�ɍi��A���̊e�ꍇ�ɂ��āA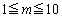 ��������m��T�����ƂɂȂ�܂��B
��������m��T�����ƂɂȂ�܂��B
�~�̒��S�����_O�C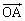 �ɉ����Ă��̕�����x���C
�ɉ����Ă��̕�����x���C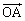 ���v����
���v����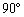 ��]����������y�����Ƃ�A�_A�̍��W��
��]����������y�����Ƃ�A�_A�̍��W��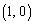 �Ƃ��܂��B
�Ƃ��܂��B
3�_P�CQ�CR���~���ɉ����Ĉړ����������́A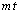 �Ct�C
�Ct�C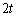 �ŁA���a��1�Ȃ̂ŁA���̋����͂��̂܂܉�]�p�̑傫���ƂȂ�AP�CQ�������v���AR�����v���ɓ������Ƃ���AP�CQ�CR�̎���t�ɂ�������W�́A
�ŁA���a��1�Ȃ̂ŁA���̋����͂��̂܂܉�]�p�̑傫���ƂȂ�AP�CQ�������v���AR�����v���ɓ������Ƃ���AP�CQ�CR�̎���t�ɂ�������W�́A
�~���ɓ��ڂ��遢PQR��PR���ΕӂƂ��钼�p�ӎO�p�`�ɂȂ邽�߂��K�v�\�������́A
PR���~�̒��a�ł����āA���A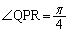
�ƂȂ邱�Ƃł����APR���~�̒��a�ł��邽�߂ɂ́A
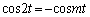 ����
���� 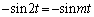 �@����@
�@����@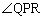 �͉~���p
�͉~���p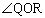 ��
��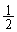 �Ȃ̂ŁA
�Ȃ̂ŁA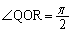
����āA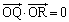 �@(�������Q��)
�@(�������Q��)
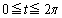 �ɂ����ẮA
�ɂ����ẮA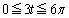 ���A
���A
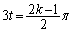 (
(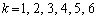 )
)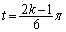 �@����A
�@����A
�@���A
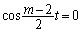 �̂Ƃ��ɂ�
�̂Ƃ��ɂ�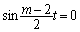 �ƂȂ蓾�Ȃ��̂ŁA���҂��Ƃ��ɐ��藧���߂ɂ́A
�ƂȂ蓾�Ȃ��̂ŁA���҂��Ƃ��ɐ��藧���߂ɂ́A
�A���A
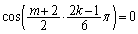 (
(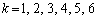 )
)
�� 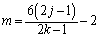 �@����B
�@����B
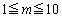 ���A
���A
�E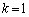 �̂Ƃ��A�C�́A
�̂Ƃ��A�C�́A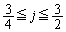
�E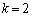 �̂Ƃ��A�C�́A
�̂Ƃ��A�C�́A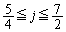
�� 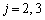
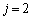 �̂Ƃ��B���A
�̂Ƃ��B���A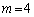
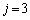 �̂Ƃ��B���A
�̂Ƃ��B���A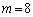
�܂��A�A���A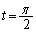
�E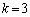 �̂Ƃ��A�C�́A
�̂Ƃ��A�C�́A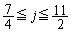
�� 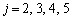 ���̂����A�B�̉E�ӕ��q��
���̂����A�B�̉E�ӕ��q��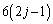 �������
�������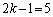 �Ŋ�����̂�
�Ŋ�����̂�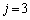 �݂̂ŁA���̂Ƃ��A
�݂̂ŁA���̂Ƃ��A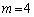
�܂��A�A���A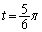
�E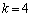 �̂Ƃ��A�C�́A
�̂Ƃ��A�C�́A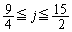
�� 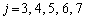 ���̂����A�B�̉E�ӕ��q��
���̂����A�B�̉E�ӕ��q��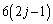 �������
�������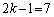 �Ŋ�����̂�
�Ŋ�����̂�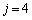 �݂̂ŁA���̂Ƃ��A
�݂̂ŁA���̂Ƃ��A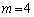
�܂��A�A���A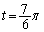
�E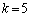 �̂Ƃ��A�C�́A
�̂Ƃ��A�C�́A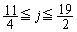
�� 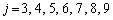 ���̂����A�B�̉E�ӕ��q��
���̂����A�B�̉E�ӕ��q��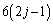 �������
�������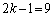 �Ŋ�����̂�
�Ŋ�����̂�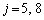 �݂̂ŁA
�݂̂ŁA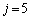 �̂Ƃ�
�̂Ƃ�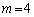 �C
�C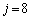 �̂Ƃ�
�̂Ƃ�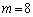
�܂��A�A���A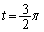
�E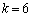 �̂Ƃ��A�C�́A
�̂Ƃ��A�C�́A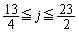
�� 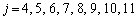 ���̂����A�B�̉E�ӕ��q��
���̂����A�B�̉E�ӕ��q��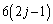 �������
�������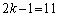 �Ŋ�����̂�
�Ŋ�����̂�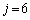 �݂̂ŁA���̂Ƃ�
�݂̂ŁA���̂Ƃ�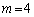
�܂��A�A���A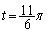
�ȏ���A
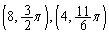 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B