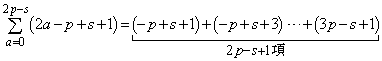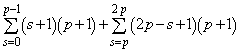���嗝�n���w'11�N�O��[5]
p�Cq��2�̐��̐����Ƃ���B����a�Cb�Cc�ŏ���
 �C
�C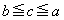
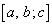 �̌`�ɕ��ׂ����̂�
�̌`�ɕ��ׂ����̂�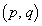 �p�^�[���ƌĂԁB�e
�p�^�[���ƌĂԁB�e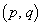 �p�^�[��
�p�^�[��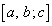 �ɑ���
�ɑ���
�Ƃ����B
(1) 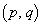 �p�^�[���̂����A
�p�^�[���̂����A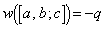 �ƂȂ���̂̌������߂�B�܂��A
�ƂȂ���̂̌������߂�B�܂��A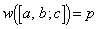 �ƂȂ�
�ƂȂ�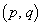 �p�^�[���̌������߂�B
�p�^�[���̌������߂�B �ȉ��A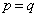 �̏ꍇ���l����B
�̏ꍇ���l����B
(2) s�𐮐��Ƃ���B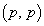 �p�^�[����
�p�^�[����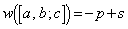 �ƂȂ���̂̌������߂�B
�ƂȂ���̂̌������߂�B (3) 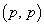 �p�^�[���̌������߂�B
�p�^�[���̌������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@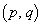 �p�^�[���̔w�i�͂킩��܂��A�v�����
�p�^�[���̔w�i�͂킩��܂��A�v�����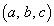 ��ԓ��̊i�q�_�𐔂�����ł��B��蕶�ɘf�킳��Ȃ���A�U�������Ă���̂ŁA�Y�ݍ��ނ��Ƃ͂Ȃ��Ǝv���܂��B�A���A�ו��ł͐_�o���g���܂��B
��ԓ��̊i�q�_�𐔂�����ł��B��蕶�ɘf�킳��Ȃ���A�U�������Ă���̂ŁA�Y�ݍ��ނ��Ƃ͂Ȃ��Ǝv���܂��B�A���A�ו��ł͐_�o���g���܂��B
����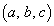 �̑g�ƁA
�̑g�ƁA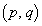 �p�^�[��
�p�^�[��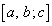 �Ƃ�1��1�őΉ����܂��B
�Ƃ�1��1�őΉ����܂��B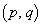 �p�^�[��
�p�^�[��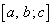 �̌��͊i�q�_
�̌��͊i�q�_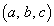 �̌��ƈ�v���܂��B
�̌��ƈ�v���܂��B
(1) 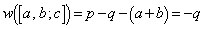
���A
���A
��蕶���̏����F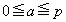 ���A
���A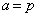 �Ɍ����܂��B���̂Ƃ��A
�Ɍ����܂��B���̂Ƃ��A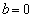
��������c�̌���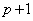 �ŁA
�ŁA
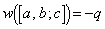 �ƂȂ�
�ƂȂ�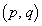 �p�^�[���̌���
�p�^�[���̌���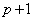 �� ......[��]
�� ......[��] ���A
���A
��蕶���̏����F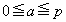 ���A
���A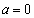 �Ɍ����܂��B���̂Ƃ��A
�Ɍ����܂��B���̂Ƃ��A
��������c�̌���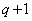 �ŁA
�ŁA
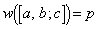 �ƂȂ�
�ƂȂ�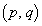 �p�^�[���̌���
�p�^�[���̌���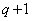 �� ......[��]
�� ......[��]
(2) 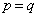 �̂Ƃ��A
�̂Ƃ��A ������A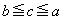 ��������c�̌�
��������c�̌�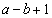 �ɂ��āA
�ɂ��āA 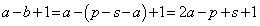 �@����@
�@����@�܂��A
���A
����ƁA��蕶���̏����F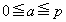 �Ƃ̋��L�������A�ȉ��ŏꍇ�������āA�l���܂��B(i)
�Ƃ̋��L�������A�ȉ��ŏꍇ�������āA�l���܂��B(i) 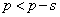 �܂���
�܂��� 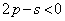 �C�����A
�C�����A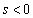 �܂���
�܂��� 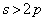 �̂Ƃ��A
�̂Ƃ��A ���L�����͑��݂����A
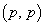 �p�^�[����
�p�^�[����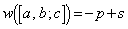 �ƂȂ���̂̌���0�� ......[��]
�ƂȂ���̂̌���0�� ......[��] (ii) 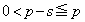 �C�����A
�C�����A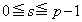 �̂Ƃ��A
�̂Ƃ��A 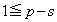 ���A
���A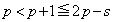 �ƂȂ�̂ŁA���L�����́A
�ƂȂ�̂ŁA���L�����́A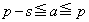 �ƂȂ�A
�ƂȂ�A
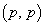 �p�^�[����
�p�^�[����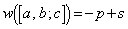 �ƂȂ���̂̌��́A�@��p���āA
�ƂȂ���̂̌��́A�@��p���āA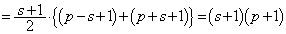 �� ......[��]
�� ......[��](iii) 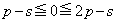 �C�����A
�C�����A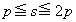 �̂Ƃ��A
�̂Ƃ��A 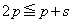 ���A
���A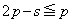 �ƂȂ�̂ŁA���L�����́A
�ƂȂ�̂ŁA���L�����́A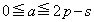 �ƂȂ�A
�ƂȂ�A
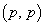 �p�^�[����
�p�^�[����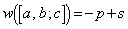 �ƂȂ���̂̌��́A�@��p���āA
�ƂȂ���̂̌��́A�@��p���āA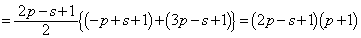 �� ......[��]
�� ......[��]
(3) (2)�ɂ����āA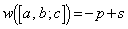 �ƂȂ�
�ƂȂ�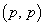 �p�^�[�������݂���̂́A(ii)��
�p�^�[�������݂���̂́A(ii)��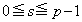 �̏ꍇ�ƁA(iii)��
�̏ꍇ�ƁA(iii)��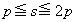 �̏ꍇ�ŁA
�̏ꍇ�ŁA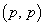 �p�^�[���̌��́A
�p�^�[���̌��́A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B