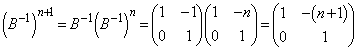���嗝�n���w'12�N�O��[5]
�s��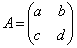 �����̏���(D)�����Ƃ���B
�����̏���(D)�����Ƃ���B
(D) A�̐���a�Cb�Cc�Cd�͐����ł���B�܂��A���ʏ��4�_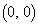 �C
�C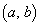 �C
�C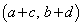 �C
�C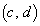 �́A�ʐ�1�̕��s�l�ӌ`��4�̒��_���Ȃ��B
�́A�ʐ�1�̕��s�l�ӌ`��4�̒��_���Ȃ��B 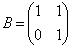 �Ƃ����B���̖₢�ɓ�����B
�Ƃ����B���̖₢�ɓ�����B
(1) �s��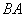 ��
��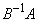 ������(D)�������Ƃ������B
������(D)�������Ƃ������B (2) 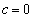 �Ȃ�AA��B�C
�Ȃ�AA��B�C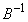 �̂ǂ��炩�������玟�X�ɂ����邱�Ƃɂ��A4�̍s��
�̂ǂ��炩�������玟�X�ɂ����邱�Ƃɂ��A4�̍s��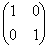 �C
�C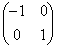 �C
�C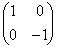 �C
�C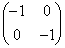 �̂ǂꂩ�ɂł��邱�Ƃ������B
�̂ǂꂩ�ɂł��邱�Ƃ������B (3) 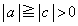 �Ƃ���B
�Ƃ���B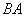 �C
�C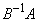 �̏��Ȃ��Ƃ��ǂ��炩����́A�����
�̏��Ȃ��Ƃ��ǂ��炩����́A�����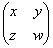 �Ƃ���ƁA
�Ƃ���ƁA �������Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�s���t�s��������(�s���[���łȂ�)�Ƃ��A�s������x�N�g����(���邢�́A�x�N�g���s)�̏W�܂�ƌ��Ȃ��Ƃ��A������1���Ɨ��ł��B�w�i�̂��肻���Ȗ��ł����A�͗e�Ղł��B
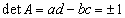 �@����@
�@����@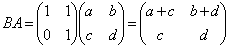
s�Ct�������Ƃ��āA
�Ƃ��܂��B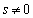 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA ���̂Ƃ��A
�ƂȂ�A�@�Ɩ����������܂��B����āA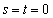 �ƂȂ�A
�ƂȂ�A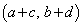 �C
�C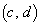 ��1���Ɨ��ŁA4�_
��1���Ɨ��ŁA4�_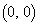 �C
�C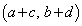 �C
�C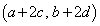 �C
�C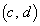 �͕��s�l�ӌ`��4�̒��_�ƂȂ�܂��B���s�l�ӌ`�̖ʐς́A
�͕��s�l�ӌ`��4�̒��_�ƂȂ�܂��B���s�l�ӌ`�̖ʐς́A �ƂȂ�A����(D)�����܂��B
s�Ct�������Ƃ���
�Ƃ��܂��B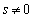 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA ���̂Ƃ��A
�ƂȂ�A�@�Ɩ����������܂��B����āA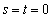 �ƂȂ�A
�ƂȂ�A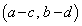 �C
�C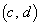 ��1���Ɨ��ŁA4�_
��1���Ɨ��ŁA4�_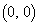 �C
�C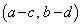 �C
�C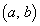 �C
�C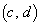 �͕��s�l�ӌ`��4�̒��_�ƂȂ�܂��B���s�l�ӌ`�̖ʐς́A
�͕��s�l�ӌ`��4�̒��_�ƂȂ�܂��B���s�l�ӌ`�̖ʐς́A �ƂȂ�A����(D)�����Ă��܂��B
(2) �܂��A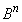 ��
��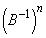 �����߂Ă����܂��B
�����߂Ă����܂��B ���A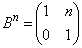 �Ɨ\���ł��܂��B
�Ɨ\���ł��܂��B ���A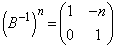 �Ɨ\���ł��܂��B
�Ɨ\���ł��܂��B ����āA�A�[�I�ɁA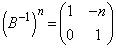
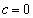 �̂Ƃ��A
�̂Ƃ��A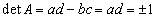 a�Cd�͐����Ȃ̂ŁA
a�Cd�͐����Ȃ̂ŁA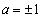 �C
�C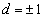 �ł����āA
�ł����āA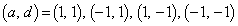 �Ɍ����܂��B
�Ɍ����܂��B 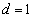 �ł����
�ł����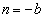 �C�܂��A
�C�܂��A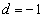 �ł����
�ł����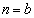 �C�Ƃ���ƁA
�C�Ƃ���ƁA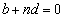 �ƂȂ�܂��B
�ƂȂ�܂��B
����āA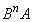 ��
��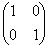 �C
�C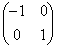 �C
�C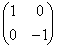 �C
�C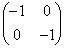 �̂ǂꂩ�ɂł��܂��B
�̂ǂꂩ�ɂł��܂��B���l�ɁA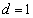 �ł����
�ł����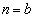 �C�܂��A
�C�܂��A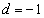 �ł����
�ł����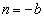 �C�Ƃ���ƁA
�C�Ƃ���ƁA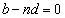 �ƂȂ�A
�ƂȂ�A
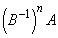 ��
��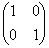 �C
�C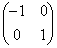 �C
�C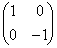 �C
�C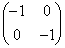 �̂ǂꂩ�ɂł��܂��B
�̂ǂꂩ�ɂł��܂��B
(3) 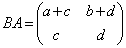
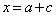 �C
�C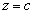
a�Cc���ٕ����ł���A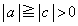 ���A
���A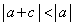
����āA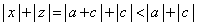
a�Cc���������ł���A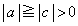 ���A
���A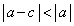
����āA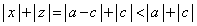
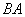 �C
�C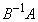 �̏��Ȃ��Ƃ��ǂ��炩����́A�����
�̏��Ȃ��Ƃ��ǂ��炩����́A�����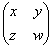 �Ƃ���ƁA
�Ƃ���ƁA �����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B