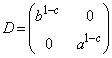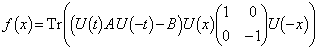東京大学理系2012年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 次の連立不等式で定まる座標平面上の領域Dを考える。
，
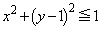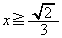
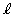は原点を通り、Dとの共通部分が線分となるものとする。その線分の長さLの最大値を求めよ。また、Lが最大値をとるとき、x軸と
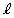のなす角θ (
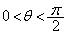)の余弦
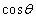を求めよ。
[解答へ]
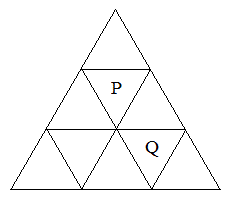[2] 図のように、正三角形を9つの部屋に辺で区切り、部屋P，Qを定める。1つの球が部屋Pを出発し、1秒ごとに、そのままその部屋にとどまることなく、辺を共有する隣の部屋に等確率で移動する。球がn秒後に部屋Qにある確率を求めよ。
[解答へ]
[3] 座標平面上で2つの不等式
，
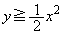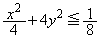
とし、y軸のまわりに回転してできる立体の体積を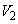
とする。
(1) 
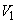と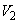
の値を求めよ。 (2) 
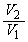の値と1の大小を判定せよ。 [解答へ]
[4] nを2以上の整数とする。自然数(1以上の整数)のn乗になる数をn乗数と呼ぶことにする。以下の問いに答えよ。
(1) 連続する2個の自然数の積はn乗数でないことを示せ。
(2) 連続するn個の自然数の積はn乗数でないことを示せ。
[解答へ]
[5] 行列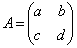
が次の条件(D)を満たすとする。
(D) Aの成分a，b，c，dは整数である。また、平面上の4点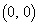
，
，
，
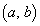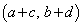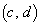は、面積1の平行四辺形の4つの頂点をなす。 
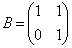とおく。次の問いに答えよ。
(1) 行列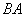
と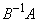
も条件(D)を満たすことを示せ。 (2) 
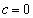ならば、AにB，
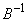のどちらかを左から次々にかけることにより、4個の行列
，
，
，
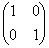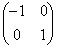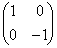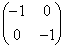のどれかにできることを示せ。 (3) 
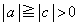とする。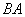
，
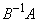の少なくともどちらか一方は、それを
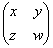とすると、 を満たすことを示せ。
[解答へ]
[6]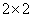 
行列
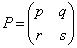に対して
と定める。
a，b，cは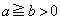
，
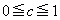を満たす実数とする。行列A，B，C，Dを次で定める。
また実数xに対し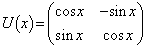
とする。
このとき以下の問いに答えよ。
(1) 各実数tに対して、xの関数
の最大値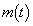
を求めよ。(ただし、最大値をとるxを求める必要はない。) (2) すべての実数tに対し
が成り立つことを示せ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。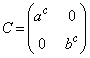 
，
，
，
