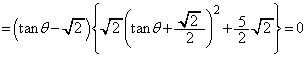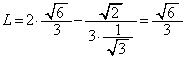���嗝�n���w'12�N�O��[1]
���̘A���s�����Œ�܂���W���ʏ�̗̈�D���l����B
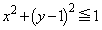 �C
�C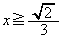
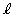 �͌��_��ʂ�AD�Ƃ̋��ʕ����������ƂȂ���̂Ƃ���B���̐����̒���L�̍ő�l�����߂�B�܂��AL���ő�l���Ƃ�Ƃ��Ax����
�͌��_��ʂ�AD�Ƃ̋��ʕ����������ƂȂ���̂Ƃ���B���̐����̒���L�̍ő�l�����߂�B�܂��AL���ő�l���Ƃ�Ƃ��Ax����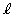 �̂Ȃ��pθ (
�̂Ȃ��pθ (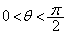 )�̗]��
)�̗]��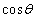 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@x����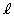 �̂Ȃ��pθ (
�̂Ȃ��pθ (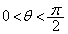 )���l����A�Ƃ����q���g�����Ă���̂ŁA���Ƃ͌v�Z����݂̂ł��B
)���l����A�Ƃ����q���g�����Ă���̂ŁA���Ƃ͌v�Z����݂̂ł��B
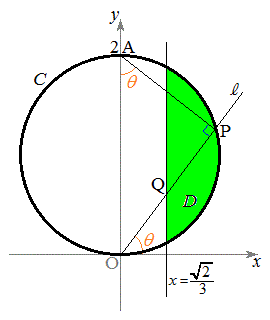 �܂��A�̈�D (�E�}���ΐF���F��)�̋��E���ɂ��āA�~C�F
�܂��A�̈�D (�E�}���ΐF���F��)�̋��E���ɂ��āA�~C�F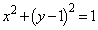 �ƒ���
�ƒ���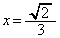 �Ƃ̌�_�����߂�ƁA
�Ƃ̌�_�����߂�ƁA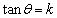 �Ƃ����ƁA����
�Ƃ����ƁA����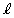 ����������
����������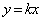 �ł��B
�ł��B
�����ŁA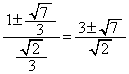 ���A
���A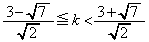 �@����@
�@����@
����Ɖ~C�Ƃ̌�_P��x���W�́A
�� 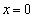 �C
�C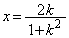
���_O�ł͂Ȃ���_��x���W�́A
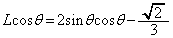 ���A
���A
���D�E�}������A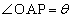 ���A
���A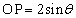
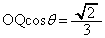 ���A
���A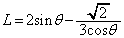
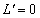 �Ƃ���ƁA
�Ƃ���ƁA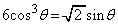
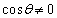 �Ȃ̂ŁA
�Ȃ̂ŁA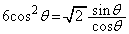 �C
�C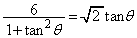
�� 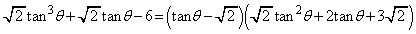
�� 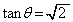
���̂Ƃ��A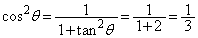 �C
�C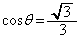 �C
�C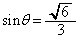
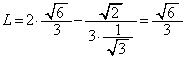
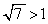 �Ȃ̂ŁA
�Ȃ̂ŁA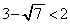 �C
�C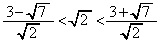 ���A
���A �C
�C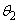 �C
�C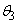 ���A
���A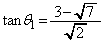 �C
�C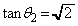 �C
�C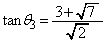 �����p�Ƃ��āA�@���
�����p�Ƃ��āA�@���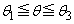 �ɂ����鑝���\�͈ȉ��̒ʂ�(���̑������Q��)�B
�ɂ����鑝���\�͈ȉ��̒ʂ�(���̑������Q��)�B
����āAL�́A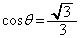 �̂Ƃ��A�ő�l�F
�̂Ƃ��A�ő�l�F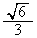 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 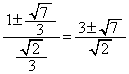 ���A
���A