���嗝�n���w'12�N�O��[2]
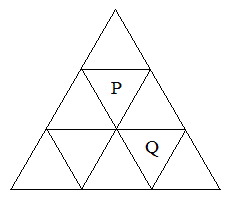 �}�̂悤�ɁA���O�p�`��9�̕����ɕӂŋ��A����P�CQ���߂�B1�̋�������P���o�����A1�b���ƂɁA���̂܂܂��̕����ɂƂǂ܂邱�ƂȂ��A�ӂ����L����ׂ̕����ɓ��m���ňړ�����B����n�b��ɕ���Q�ɂ���m�������߂�B
�}�̂悤�ɁA���O�p�`��9�̕����ɕӂŋ��A����P�CQ���߂�B1�̋�������P���o�����A1�b���ƂɁA���̂܂܂��̕����ɂƂǂ܂邱�ƂȂ��A�ӂ����L����ׂ̕����ɓ��m���ňړ�����B����n�b��ɕ���Q�ɂ���m�������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@9��������܂����A���܂��l���čs���A9�̐���̘A���Q�����ɂ��邱�Ƃ��Ȃ��A2���ԑQ�����ʼn����ł��܂��B
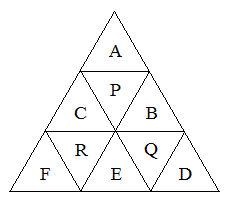 �E�}�̂悤��9�����ɖ��O�����܂��B��b��ɋ�������P�C����Q�C����R�ɂ��邱�Ƃ͂Ȃ��A�����b��ɂ́A���́A����P�C����Q�C����R�̂����ꂩ�ɗ��܂��B�܂��A�Ώ̐����l����ƁA����Q�ƕ���R�ɗ����m���͓����ł��B����P�ɗ���m�����l����A����Q�ɗ���m���͗]���ۂ̊m���Ƃ��đ����邱�Ƃ��ł��āA�Q�����𗧂Ă邱�Ƃ��ł������ł��B
�E�}�̂悤��9�����ɖ��O�����܂��B��b��ɋ�������P�C����Q�C����R�ɂ��邱�Ƃ͂Ȃ��A�����b��ɂ́A���́A����P�C����Q�C����R�̂����ꂩ�ɗ��܂��B�܂��A�Ώ̐����l����ƁA����Q�ƕ���R�ɗ����m���͓����ł��B����P�ɗ���m�����l����A����Q�ɗ���m���͗]���ۂ̊m���Ƃ��đ����邱�Ƃ��ł��āA�Q�����𗧂Ă邱�Ƃ��ł������ł��B
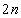 �b��ɋ�������P�ɂ���m����
�b��ɋ�������P�ɂ���m����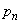 �Ƃ��܂��B�ŏ��ɕ���P�ɂ������̂ŁA
�Ƃ��܂��B�ŏ��ɕ���P�ɂ������̂ŁA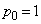 �Ƃ��܂��B
�Ƃ��܂��B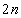 �b��ɋ�������Q�ɂ���m����
�b��ɋ�������Q�ɂ���m����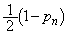 �ł��B
�ł��B
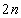 �b��ɋ�������P�ɂ���Ƃ�(�m��
�b��ɋ�������P�ɂ���Ƃ�(�m��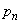 )�A
)�A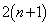 �b��ɂ���������P�ɂ���̂́A
�b��ɂ���������P�ɂ���̂́A
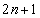 �b��ɕ���A�ɍs��(�m��
�b��ɕ���A�ɍs��(�m��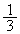 )�A
)�A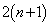 �b��ɕ���P�ɖ߂�(�m��1)���A
�b��ɕ���P�ɖ߂�(�m��1)���A
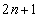 �b��ɕ���B�ɍs��(�m��
�b��ɕ���B�ɍs��(�m��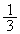 )�A
)�A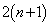 �b��ɕ���P�ɖ߂�(�m��
�b��ɕ���P�ɖ߂�(�m��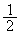 )���A
)���A
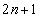 �b��ɕ���C�ɍs��(�m��
�b��ɕ���C�ɍs��(�m��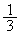 )�A
)�A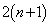 �b��ɕ���P�ɖ߂�(�m��
�b��ɕ���P�ɖ߂�(�m��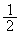 )�A
)�A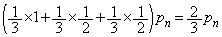
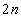 �b��ɋ�������Q�ɂ���Ƃ�(�m��
�b��ɋ�������Q�ɂ���Ƃ�(�m��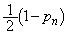 )�A
)�A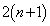 �b��ɋ�������P�ɗ���̂́A
�b��ɋ�������P�ɗ���̂́A
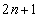 �b��ɕ���B�ɍs��(�m��
�b��ɕ���B�ɍs��(�m��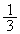 )�A
)�A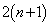 �b��ɕ���P�ɗ���(�m��
�b��ɕ���P�ɗ���(�m��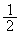 )
)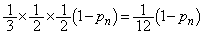
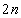 �b��ɋ�������R�ɂ���Ƃ�(�m��
�b��ɋ�������R�ɂ���Ƃ�(�m��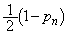 )�A
)�A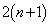 �b��ɋ�������P�ɗ���̂����l�ɁA���̊m����
�b��ɋ�������P�ɗ���̂����l�ɁA���̊m����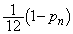
����āA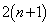 �b��ɋ�������P�ɂ���m��
�b��ɋ�������P�ɂ���m��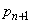 �́A
�́A
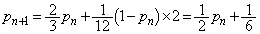 �@����@
�@����@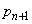 ��
��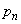 ���Ƃ���α�Ƃ���ƁA
���Ƃ���α�Ƃ���ƁA
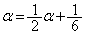 �@����A�@��
�@����A�@�� 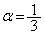
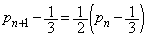
����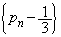 �́A�����F
�́A�����F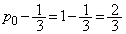 �C����F
�C����F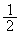 �����䐔���ł��B
�����䐔���ł��B
�� 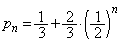
����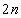 �b��ɕ���Q�ɂ���m���́A
�b��ɕ���Q�ɂ���m���́A
����āA����n�b��ɕ���Q�ɂ���m���́A
n����̂Ƃ�0�Cn�������̂Ƃ��A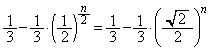 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 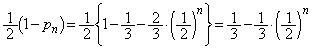
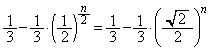 ......[��]
......[��]