���嗝�n���w'12�N�O��[3]
���W���ʏ��2�̕s����
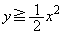 �C
�C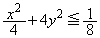
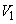 �Ƃ��Ay���̂܂��ɉ�]���Ăł��闧�̂̑̐ς�
�Ƃ��Ay���̂܂��ɉ�]���Ăł��闧�̂̑̐ς�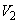 �Ƃ���B
�Ƃ���B
(1) 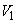 ��
��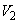 �̒l�����߂�B
�̒l�����߂�B (2) 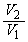 �̒l��1�̑召�肹��B
�̒l��1�̑召�肹��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�͕��}�ȋ��ϖ��ł��B(2)�̐��l�]�������嗝�n�ł͒�^�p�^�[���ő債�����Ƃ͂���܂���B
(1) �̈�S�̋��E���A
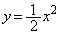 �@����@
�@����@
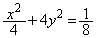 �@����A�@(�ȉ~���Q��)
�@����A�@(�ȉ~���Q��)�̌�_�����߂܂��B
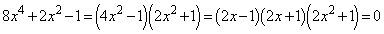 ��
�� 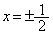 ���̂Ƃ��A
���̂Ƃ��A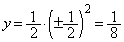
�A��y���Ƃ̌�_�́A�A��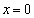 �Ƃ��āA
�Ƃ��āA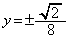
�̈�S��x���̂܂��ɉ�]����ƁA�A��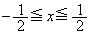 �̕�������]���Ăł��闧�̂���@��
�̕�������]���Ăł��闧�̂���@��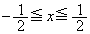 �̕�������]���Ăł��闧�̂���菜�������̂ɂȂ�܂��B
�̕�������]���Ăł��闧�̂���菜�������̂ɂȂ�܂��B
�@���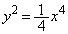 �C�A���
�C�A���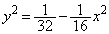
����āA���̑̐�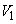 �́A�̈�S��y���Ɋւ��đΏ̂ł��邱�Ƃ���A
�́A�̈�S��y���Ɋւ��đΏ̂ł��邱�Ƃ���A�̈�S��y���̂܂��ɉ�]����ƁA�@��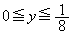 �̕�������]���Ăł��闧�̂ƁA�A��
�̕�������]���Ăł��闧�̂ƁA�A��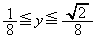 �̕�������]���Ăł��闧�̂����킹�����̂ɂȂ�܂��B
�̕�������]���Ăł��闧�̂����킹�����̂ɂȂ�܂��B
�@���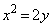 �C�A���
�C�A���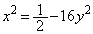
����āA���̑̐�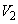 �́A
�́A
(2) 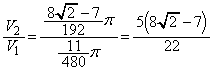
�Ȃ̂ŁA�ȉ��̂悤�ɓ��Ă��������ƂɂȂ�܂��B
���A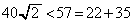
�� 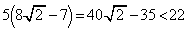 �]���āA
�]���āA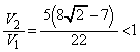 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 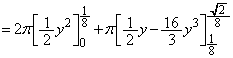
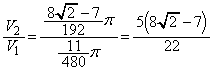
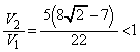 ......[��]
......[��]