���嗝�n���w'12�N�O��[4]
n��2�ȏ�̐����Ƃ���B���R��(1�ȏ�̐���)��n��ɂȂ鐔��n�搔�ƌĂԂ��Ƃɂ���B�ȉ��̖₢�ɓ�����B
(1) �A������2�̎��R���̐ς�n�搔�łȂ����Ƃ������B
(2) �A������n�̎��R���̐ς�n�搔�łȂ����Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�u�E�E�E�łȂ����Ƃ������v�Ƃ�����蕶�ł́A�w���@�̗��p���l���܂��B�Ȃ��A�������Q�Ƃ��Ă��������B
(1) �A������2�̎��R��k�C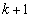 �̐ς�n�搔���Ɖ��肵�܂��B
�̐ς�n�搔���Ɖ��肵�܂��B k��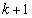 �݂͌��ɑf��1�ȊO�̋��ʂ̖������Ȃ��̂ŁA
�݂͌��ɑf��1�ȊO�̋��ʂ̖������Ȃ��̂ŁA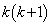 ��n�搔�ł���Ap�Cq�����R���Ƃ��āA
��n�搔�ł���Ap�Cq�����R���Ƃ��āA �ƕ\���܂��B�����ŁA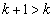 ���
���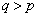 �ł��B
�ł��B 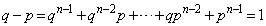 �@����@
�@����@�Ɍ����܂��B�Ƃ���ŁA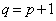 �ł���A
�ł���A ����n���̘a�̊e���͂������1�ȏ�ŁA
�ŁA�@�Ɩ����������܂��B�]���āA����͌��ŁA�A������2�̎��R���̐ς�n�搔�ł͂���܂���B
(2) 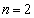 �̂Ƃ���(1)�ŏؖ�����Ă��܂��B
�̂Ƃ���(1)�ŏؖ�����Ă��܂��B 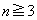 �̂Ƃ��A�A������n�̎��R��k�A
�̂Ƃ��A�A������n�̎��R��k�A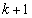 �C
�C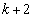 �C����C
�C����C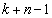 �̐ς�n�搔���Ɖ��肵�܂��Bp�����R���Ƃ��āA
�̐ς�n�搔���Ɖ��肵�܂��Bp�����R���Ƃ��āA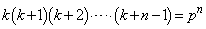 �@����A
�@����A�ƕ\���܂��B
���A
�ł��B����āAi��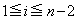 ���������ꂩ�̐���(
���������ꂩ�̐���(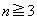 ���)�Ƃ��āA
���)�Ƃ��āA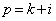 �ł��B�A�́A
�ł��B�A�́A �ƂȂ�܂����A����ł́A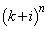 �C����
�C����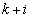 ���A
���A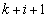 (
(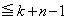 )�Ŋ����邱�ƂɂȂ�܂��B
)�Ŋ����邱�ƂɂȂ�܂��B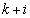 ��
��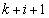 �݂͌��ɑf�Ȃ̂ŁA�����������܂��B����āA�A����p�͑��݂����A�A������n�̐ς�n�搔�ł͂���܂���B
�݂͌��ɑf�Ȃ̂ŁA�����������܂��B����āA�A����p�͑��݂����A�A������n�̐ς�n�搔�ł͂���܂���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B