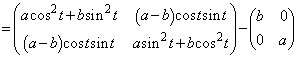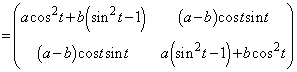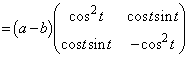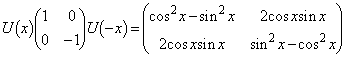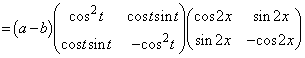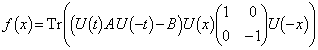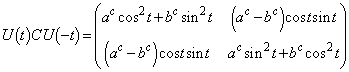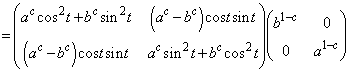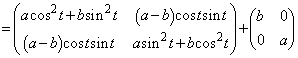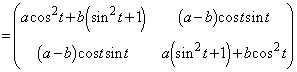���嗝�n���w'12�N�O��[6]
 �s��
�s��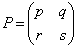 �ɑ���
�ɑ���
�ƒ�߂�B
a�Cb�Cc��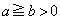 �C
�C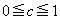 ���������Ƃ���B�s��A�CB�CC�CD�����Œ�߂�B
���������Ƃ���B�s��A�CB�CC�CD�����Œ�߂�B
�܂�����x�ɑ�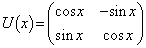 �Ƃ���B
�Ƃ���B
���̂Ƃ��ȉ��̖₢�ɓ�����B
(1) �e����t�ɑ��āAx�̊�
�̍ő�l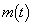 �����߂�B(�������A�ő�l���Ƃ�x�����߂�K�v�͂Ȃ��B)
�����߂�B(�������A�ő�l���Ƃ�x�����߂�K�v�͂Ȃ��B) (2) ���ׂĂ̎���t�ɑ�
�����藧���Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@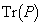 �͑Ίp�a�ƌĂ�A�s��P�̑Ίp�����̘a�ɂȂ�܂��B2�������s��ł́A
�͑Ίp�a�ƌĂ�A�s��P�̑Ίp�����̘a�ɂȂ�܂��B2�������s��ł́A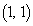 ������
������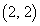 �����̘a�ɂȂ�܂��B
�����̘a�ɂȂ�܂��B
�{��́A�r���̌v�Z�����Ȃ�ʓ|�ŁA��Â����m�Ȍv�Z�͂��v������܂��B
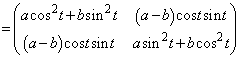 �@����@
�@����@�@�ɂ����āA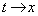 �C
�C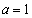 �C
�C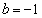 �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A �����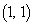 �����́A
�����́A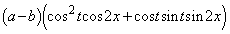
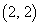 �����́A
�����́A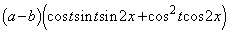
����āA 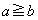 �Ȃ̂ŁA
�Ȃ̂ŁA
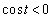 �̂Ƃ��A
�̂Ƃ��A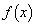 �́A
�́A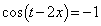 �̂Ƃ��ɍő�l�F
�̂Ƃ��ɍő�l�F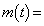
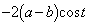 ���Ƃ�܂��B
���Ƃ�܂��B
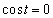 �̂Ƃ��A
�̂Ƃ��A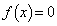 �Ȃ̂�
�Ȃ̂�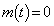 �ł��B
�ł��B
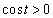 �̂Ƃ��A
�̂Ƃ��A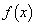 �́A
�́A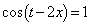 �̂Ƃ��ɍő�l�F
�̂Ƃ��ɍő�l�F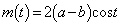 ���Ƃ�܂��B
���Ƃ�܂��B
�ȏ���A3�ʂ�̏ꍇ���܂Ƃ߂āA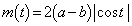 ......[��]
......[��]
(2) �@�ŁA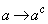 �C
�C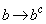 �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A �����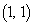 �����́A
�����́A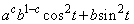
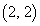 �����́A
�����́A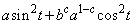
����āA �ȏ���A
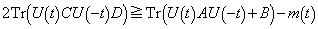 �@����A
�@����A��
��
��
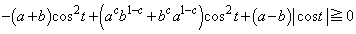 �@����B
�@����B���̍��ӂ́A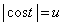 (
(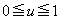 )�Ƃ����ƁA
)�Ƃ����ƁA 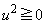 ���A
���A�Ƃ����ƁA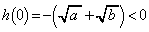 �C
�C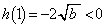 ���A
���A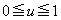 �ɂ����āA
�ɂ����āA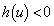
�]���āA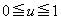 �ɂ����āA
�ɂ����āA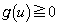
����āA�B�����藧�̂ŇA�����藧���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 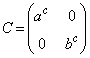 �C
�C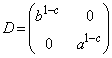
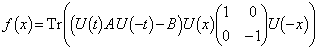
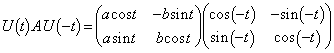
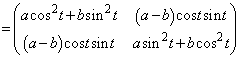 �@����@
�@����@