���啶�n���w'13�N[1]
��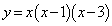 �̃O���t��C�C���_O��ʂ�X��t�̒�����
�̃O���t��C�C���_O��ʂ�X��t�̒�����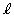 �Ƃ��AC��
�Ƃ��AC��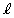 ��O�ȊO�ɋ��L�_�����Ƃ���BC��
��O�ȊO�ɋ��L�_�����Ƃ���BC��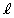 �̋��L�_��O�CP�CQ�Ƃ��A
�̋��L�_��O�CP�CQ�Ƃ��A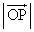 ��
��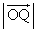 �̐ς�
�̐ς�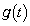 �Ƃ����B�������A����狤�L�_��1���ړ_�ł���ꍇ�́AO�CP�CQ�̂�����2����v���āA���̐ړ_�ł���Ƃ���B��
�Ƃ����B�������A����狤�L�_��1���ړ_�ł���ꍇ�́AO�CP�CQ�̂�����2����v���āA���̐ړ_�ł���Ƃ���B��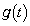 �̑����ׁA���̋ɒl�����߂�B
�̑����ׁA���̋ɒl�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ɒl�̌v�Z�ȂǁA�Z�I��v����ʂ͂���܂����A�قƂ�Ǎl����Ƃ���̂Ȃ��A�P�ɖʓ|�Ȍv�Z���ł��B
�@�C�A��A������ƁA
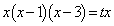
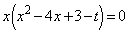 �@����B
�@����B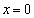 �܂���
�܂��� 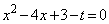
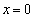 �ȊO�Ɏ����������̂ŁA
�ȊO�Ɏ����������̂ŁA
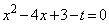 �@����C �̔��ʎ��F
�@����C �̔��ʎ��F
�� 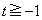 �@����D
�@����D
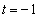 �̂Ƃ��ɂ͏d���ƂȂ�A
�̂Ƃ��ɂ͏d���ƂȂ�A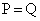 �ƂȂ�܂��B
�ƂȂ�܂��B
�D��2����p�Cq�Ƃ��āA���ƌW���̊W���A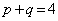 �C
�C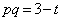
P�CQ�̍��W��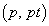 �C
�C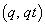 �Ƃ��āA
�Ƃ��āA
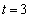 �̂Ƃ��A�C��
�̂Ƃ��A�C��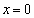 �����ɂ����A�B�͏d��
�����ɂ����A�B�͏d��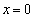 �������܂��B�܂�A���̂Ƃ��A
�������܂��B�܂�A���̂Ƃ��A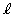 ��C��
��C��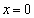 �Őڂ��Ă��܂��BP
�Őڂ��Ă��܂��BP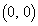 �CQ
�CQ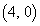 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA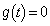 �ƂȂ�킯�ł��B
�ƂȂ�킯�ł��B
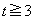 �̂Ƃ��A
�̂Ƃ��A
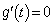 �Ƃ���ƁA
�Ƃ���ƁA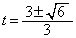 (�������}�ǂ���ł����Ă�
(�������}�ǂ���ł����Ă�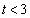 �ł�)
�ł�)
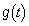 ��
��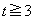 �͈̔͂ɋɒl���������A���͈̔͂�
�͈̔͂ɋɒl���������A���͈̔͂�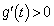 ���A
���A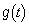 �͒P�������ł��B
�͒P�������ł��B
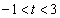 �̂Ƃ��A
�̂Ƃ��A
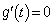 �Ƃ���ƁA
�Ƃ���ƁA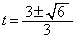
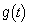 ��
��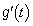 �Ŋ���ƁA����
�Ŋ���ƁA����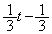 �C�]���
�C�]���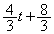 �ɂȂ�̂ŁA
�ɂȂ�̂ŁA
�����ŁA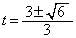 (
(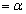 �Ƃ��܂�)�Ƃ���ƁA
�Ƃ��܂�)�Ƃ���ƁA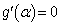 ���A
���A
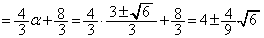 (��������)
(��������)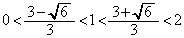 ���A
���A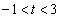 �C
�C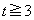 ���킹�đ����\�͈ȉ��̂悤�ɂȂ�܂��B
���킹�đ����\�͈ȉ��̂悤�ɂȂ�܂��B
�����\���(3�����̑������Q��)�A�ɒl�́A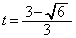 �̂Ƃ��ɏ��l
�̂Ƃ��ɏ��l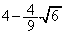 �C
�C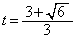 �̂Ƃ��ɑ�l
�̂Ƃ��ɑ�l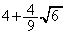 �C
�C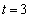 �̂Ƃ��ɏ��l0 ......[��]
�̂Ƃ��ɏ��l0 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B