���嗝�n���w'84�N[6]
xy���ʂɂ����āA�s����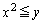 �̕\���̈��D�Ƃ��A�s����
�̕\���̈��D�Ƃ��A�s����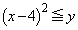 �̕\���̈��E�Ƃ���B���̂Ƃ��A���̏���(��)�����_P
�̕\���̈��E�Ƃ���B���̂Ƃ��A���̏���(��)�����_P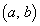 �S�̂̏W�������߁A�����}������B
�S�̂̏W�������߁A�����}������B
(��)�@P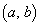 �Ɋւ���D�ƑΏ̂ȗ̈��U�Ƃ���Ƃ��A
�Ɋւ���D�ƑΏ̂ȗ̈��U�Ƃ���Ƃ��A �������ɐ��藧�B�������A �͋�W����\�����̂Ƃ���B
�͋�W����\�����̂Ƃ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�̈��ɂ��Ă̏����ɂȂ��Ă��܂����A���E���ɂ��Ă̏����Ƃ��čl�����OK�ł��B
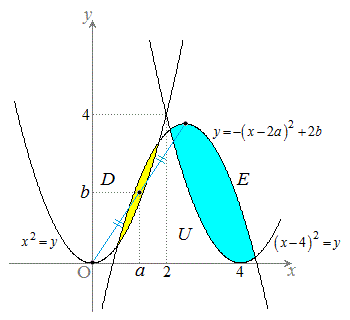
�E�}�ɁA��蕶�̏������܂��B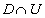 �͉��F���F�����A
�͉��F���F�����A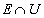 �͐��F���F�����ł��B
�͐��F���F�����ł��B
D�̋��E��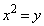 ��̓_��
��̓_��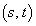 �Ƃ��āA�����P
�Ƃ��āA�����P �Ɋւ��đΏ̂ȓ_��
�Ɋւ��đΏ̂ȓ_��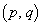 �Ƃ��܂��B
�Ƃ��܂��B
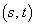 ��
��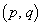 �̒��_��
�̒��_��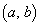 �ɂȂ�̂ŁA
�ɂȂ�̂ŁA
�����藧���܂��B������A
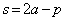 �C
�C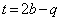 �@����@
�@����@
�����̂ŁA�����ɇ@��������ƁA
�� 
������AU�̋��E���́A
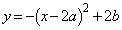 �@����A
�@����A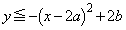 �����܂��B�A�̉E�ӂ�
�����܂��B�A�̉E�ӂ�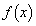 �Ƃ����܂��B
�Ƃ����܂��B
�����ŁAD�̋��E��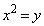 ��E�̋��E��
��E�̋��E��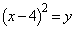 �̌�_�����߂Ă����܂��B
�̌�_�����߂Ă����܂��B
������A�����āA
�� 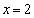 �C
�C
��_��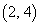 �ł��B
�ł��B
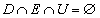 �����藧�A�Ƃ������Ƃ́AU�̋��E���A�́A���̌�_
�����藧�A�Ƃ������Ƃ́AU�̋��E���A�́A���̌�_ ��������ʂ�A�Ƃ������Ƃł��B�܂�A
��������ʂ�A�Ƃ������Ƃł��B�܂�A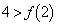 ���A
���A
�� 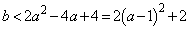 �@����B
�@����B
����ɁA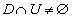 �����藧�A�Ƃ������Ƃ́AU�̋��E���A��
�����藧�A�Ƃ������Ƃ́AU�̋��E���A��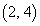 ��������ʂ邱�Ƃ��l������ƁAD�̋��E��
��������ʂ邱�Ƃ��l������ƁAD�̋��E��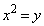 ��U�̋��E���A��
��U�̋��E���A��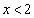 �ɂ�����2���L�_(1�ړ_�̏ꍇ���܂�)�������ƂƓ��l�ł���A
�ɂ�����2���L�_(1�ړ_�̏ꍇ���܂�)�������ƂƓ��l�ł���A
����ɁA �ƇA��A�������ē�����2���������F
�ƇA��A�������ē�����2���������F
�����A
�� �ƂȂ�2������(�d�����܂�)�������ƂƓ��l�ł���A
�ƂȂ�2������(�d�����܂�)�������ƂƓ��l�ł���A
�]���āA���̍��ӂ�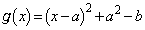 �Ƃ����āA
�Ƃ����āA
���ʎ��F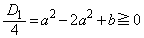 ����
���� 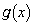 �̎��F
�̎��F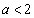 ���� ��Ԃ̒[�F
���� ��Ԃ̒[�F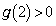
�Ɠ��l�ł�(2���������̉��̔z�u���Q��)�B
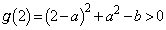 �� �B
�� �B
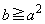 ����
���� 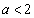 �@����C
�@����C
���l�ɁA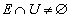 �����藧���Ƃ��AU�̋��E���A��
�����藧���Ƃ��AU�̋��E���A��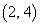 ��������ʂ邱�Ƃ��l������ƁA
��������ʂ邱�Ƃ��l������ƁA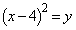 �ƇA��A�������Ăł���2���������F
�ƇA��A�������Ăł���2���������F
�����A
���A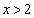 �ƂȂ�2������(�d�����܂�)�������Ɠ��l�ł���A
�ƂȂ�2������(�d�����܂�)�������Ɠ��l�ł���A
�]���āA���̍��ӂ�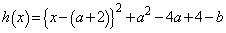 �Ƃ����āA
�Ƃ����āA
���� ��Ԃ̒[�F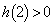
�Ɠ��l�ł��B
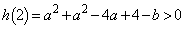 �� �B
�� �B
 ����
���� 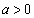 �@����D
�@����D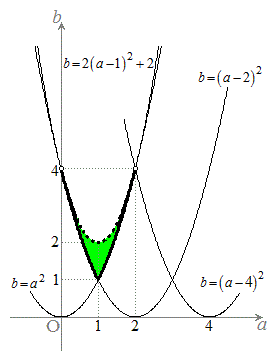
�B ���� �C ���� �D�C���A
�}������ƉE�}���ΐF���F��(��������܂ݔ��}���Ɣj������܂܂Ȃ�)�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B