���嗝�H���w'07�N[4]
n�𐳂̐����Ƃ���Ƃ��A�ȉ��̖�ɓ�����B
(1) k�𐳂̐����Ƃ���B��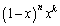 ��
��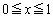 �ɂ�����ő�l��
�ɂ�����ő�l��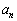 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A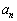 �����
�����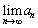 �����߂�B
�����߂�B (2) 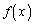 �C
�C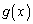 ��
��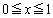 �ɂ����Ē�߂�ꂽ�A�����Ƃ���B��
�ɂ����Ē�߂�ꂽ�A�����Ƃ���B��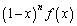 �C
�C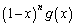 �C
�C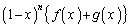 ��
��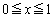 �ɂ�����ő�l�����ꂼ��
�ɂ�����ő�l�����ꂼ��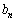 �C
�C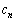 �C
�C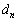 �Ƃ���B���̂Ƃ�0�C
�Ƃ���B���̂Ƃ�0�C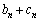 �C
�C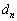 �̑召��
�̑召�� �@�@�@�@�@���@�@���@�@
�̌`���œ����A���̗��R���ׂ̂�B
(3) 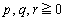 ��萔�A
��萔�A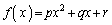 �Ƃ��A��
�Ƃ��A��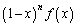 ��
��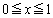 �ɂ�����ő�l��
�ɂ�����ő�l��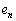 �Ƃ���B���̂Ƃ�
�Ƃ���B���̂Ƃ�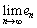 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����������͓��Ɍ����Ă��܂��̂ł����A��₾�Ǝv���Ă��܂��Ɠ��ł��B
(1) 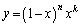
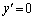 �Ƃ���ƁA
�Ƃ���ƁA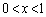 �ɂ����ẮA
�ɂ����ẮA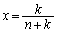 �@(
�@(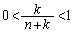 )
)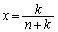 �̂Ƃ��A
�̂Ƃ��A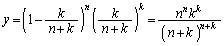 �����\���A
�����\���A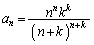 ......[��]�܂��A
......[��]�܂��A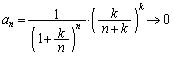 �@(��
�@(�� 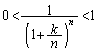 �C
�C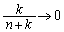 )��
)�� 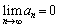 ......[��]
......[��]
(2) 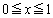 �ɂ����āA��
�ɂ����āA��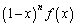 �C
�C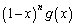 �C
�C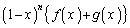 ���A���ꂼ��A
���A���ꂼ��A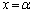 �C
�C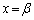 �C
�C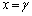 (
(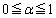 �C
�C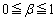 �C
�C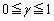 )�ɂ����āA�ő�ɂȂ�Ƃ���ƁA
)�ɂ����āA�ő�ɂȂ�Ƃ���ƁA �@�{�A���A
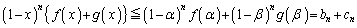 �@����C
�@����C�B�̕s�����̓����́A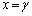 �̂Ƃ��ɐ������܂��B
�̂Ƃ��ɐ������܂��B
�C�̕s�����̓����́A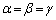 �ł���A
�ł���A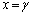 �̂Ƃ��ɐ������܂����A����ȊO�̏ꍇ�ɂ́A�K��������������Ƃ͌��Ȃ����Ƃɒ��ӂ��Ă��������B
�̂Ƃ��ɐ������܂����A����ȊO�̏ꍇ�ɂ́A�K��������������Ƃ͌��Ȃ����Ƃɒ��ӂ��Ă��������B
�C���ӂŁA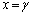 �̂Ƃ����l����ƁA
�̂Ƃ����l����ƁA 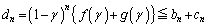 �@����D
�@����D�܂��A��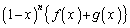 �́A
�́A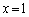 �̂Ƃ��ɁA���l0���Ƃ�܂��B�]���āA���̍ő�l
�̂Ƃ��ɁA���l0���Ƃ�܂��B�]���āA���̍ő�l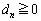 �@����E
�@����E
�D�C�E���A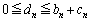 ......[��]
......[��]
(3) ��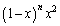 �C
�C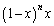 ��
��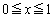 �ɂ�����ő�l��
�ɂ�����ő�l��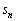 �C
�C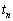 �Ƃ���ƁA
�Ƃ���ƁA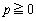 �C
�C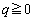 ���A��
���A��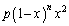 �C
�C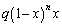 ��
��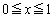 �ɂ�����ő�l�́A
�ɂ�����ő�l�́A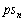 �C
�C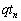 �ł��B
�ł��B �܂��A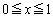 �ɂ����āA
�ɂ����āA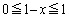 �C
�C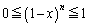 ���A
���A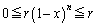 �@(
�@(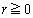 )��
)��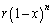 ��
��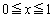 �ɂ�����ő�l�́A
�ɂ�����ő�l�́A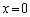 �̂Ƃ��Ar�ł��B
�̂Ƃ��Ar�ł��B
��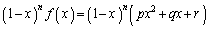 ��
��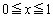 �ɂ�����ő�l
�ɂ�����ő�l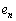 �ɂ��āA(2)�̌��ʂ��A
�ɂ��āA(2)�̌��ʂ��A 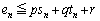 �@����F
�@����F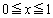 �ɂ����āA
�ɂ����āA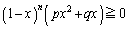 ���A���F
���A���F��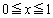 �ɂ�����ő�l
�ɂ�����ő�l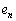 �́A��
�́A��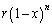 �̍ő�lr�ȏ�ł����āA
�̍ő�lr�ȏ�ł����āA 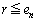 �@����G
�@����G
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B