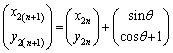���勳�琔�w'08�N[4]
���W���ʏ�Ŏ��̂悤�ȕϊ�f���l����B
f�F���_�𒆐S�Ƃ��Đ��̌����Ɋpθ ������]���Ay���ɂ��đΏ̈ړ������Ay���̐�������1�������s�ړ�����B
�_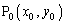 �ɕϊ�f��n��J��Ԃ��s���ē�����_��
�ɕϊ�f��n��J��Ԃ��s���ē�����_��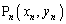 �ƕ\���B���̖₢�ɓ�����B
�ƕ\���B���̖₢�ɓ�����B
(2)  �Ȃ�A�_�̗�
�Ȃ�A�_�̗�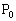 �C
�C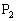 �C
�C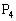 �C����C
�C����C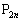 �C��� �́A���钼����ɓ������Ԋu�ŕ��Ԃ��Ƃ������B
�C��� �́A���钼����ɓ������Ԋu�ŕ��Ԃ��Ƃ������B (3) 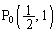 �Ƃ���B���ׂĂ̓_
�Ƃ���B���ׂĂ̓_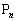 (
(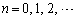 )��1�̒�����ɕ��Ԃ悤��θ �̒l�����߂�B�������A
)��1�̒�����ɕ��Ԃ悤��θ �̒l�����߂�B�������A �Ƃ���B
�Ƃ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�x�N�g��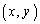 ���A2�s1����s���Ƃ���
���A2�s1����s���Ƃ���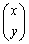 �Ə������Ƃɂ��܂��B
�Ə������Ƃɂ��܂��B
���̖��́A�_���I�ɂ�₱�����ł����A���ۂ̍�Ƃ͌v�Z����ł��B�Z�C���N�������ɔE�ϋ������g��ł��������B
(1)�́A���̖��ł́A���܂���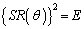 �ɂȂ�̂Řb���ȒP�ɂ��݂܂����A�ӂ���2���ԑQ�����̂悤�ɂ���Ă������ƂɂȂ�ł��傤�B
�ɂȂ�̂Řb���ȒP�ɂ��݂܂����A�ӂ���2���ԑQ�����̂悤�ɂ���Ă������ƂɂȂ�ł��傤�B
�Ȃ��A1���ϊ����Q�Ƃ��Ă��������B
(1) �܂��A�_ �ɕϊ�f���{���Ƃǂ��Ȃ邩�A�Ƃ������Ƃׂ܂��B
�ɕϊ�f���{���Ƃǂ��Ȃ邩�A�Ƃ������Ƃׂ܂��B 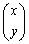 �����_�𒆐S�Ƃ��Đ��̌����Ɋpθ ������]����ƁA��]��\���s����
�����_�𒆐S�Ƃ��Đ��̌����Ɋpθ ������]����ƁA��]��\���s����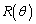 �Ƃ��āA
�Ƃ��āA�ɗ��܂��B�����y���ɂ��đΏ̈ړ�����ƁAx���W�̕������ς��A�Ώ̈ړ���\���s���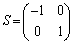 �Ƃ��āA
�Ƃ��āA �ɗ��܂��B����ɁAy����������1�������s�ړ�����ƁAy���W��1�������āA
�ɗ��܂��B
�_ �ɑ��ĕϊ�f���s����
�ɑ��ĕϊ�f���s����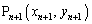 �ɗ���Ƃ���ƁA
�ɗ���Ƃ���ƁA 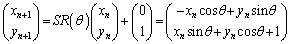 �@����@
�@����@�����ŁA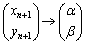 �C
�C �ƒu�������āA2���ԑQ�����̂悤�ɂł��Ȃ����A�Ƃ����A�C�f�A�������т܂����A
�ƒu�������āA2���ԑQ�����̂悤�ɂł��Ȃ����A�Ƃ����A�C�f�A�������т܂����A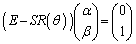 �ƂȂ����Ƃ��ɁA
�ƂȂ����Ƃ��ɁA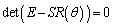 �ƂȂ�A
�ƂȂ�A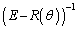 �����݂��Ȃ��̂ŁA���܂��s���܂���(�t�s���݂���悤�Ȗ��Ȃ�A�s��̗ݏ�����߂邱�Ƃɂ��A2���ԑQ�����̂悤�ɉ������Ƃ��ł��܂�)�B
�����݂��Ȃ��̂ŁA���܂��s���܂���(�t�s���݂���悤�Ȗ��Ȃ�A�s��̗ݏ�����߂邱�Ƃɂ��A2���ԑQ�����̂悤�ɉ������Ƃ��ł��܂�)�B
�����ł́A�@���J��Ԃ��p���܂��B ������
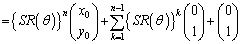 �@����A
�@����A�Ƃ���ŁA
���A
(a) m�����̊�̂Ƃ��A
(b) m�����̋����̂Ƃ��A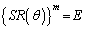
�����ŁAn������������ŏꍇ�������āA
(i) n����̂Ƃ��A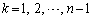 �̒��ɁA��A�����Ƃ��ɁA
�̒��ɁA��A�����Ƃ��ɁA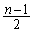 ������̂ŁA�A���A
������̂ŁA�A���A �� 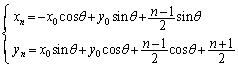 ......[��]
......[��] (ii) n�������̂Ƃ��A �̒��ɁA���
�̒��ɁA��� �A������
�A������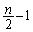 ����̂ŁA�A���A
����̂ŁA�A���A 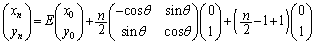 ��
�� 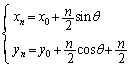 ......[��]
......[��]
(2) (1)(ii)�̌��ʂ�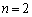 �Ƃ��āA
�Ƃ��āA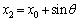 �C
�C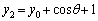
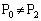 ���A
���A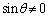 �C
�C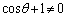
����āA(1)(ii)�̌��ʂ�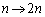 �Ƃ��āA
�Ƃ��āA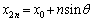 �@����B
�@����B
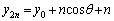 �@����C
�@����C�B�~ �|�C�~
�|�C�~ �Ƃ��āAn����������ƁA
�Ƃ��āAn����������ƁA ����́A�_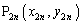 ���A�����F
���A�����F 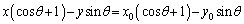 �@����D
�@����D�̏�ɂ��邱�Ƃ��Ӗ����܂��B�܂��A
���A�_�̗� �C
�C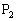 �C
�C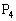 �C����C
�C����C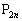 �C��� �́A�����D��ɁA���Ԋu�F
�C��� �́A�����D��ɁA���Ԋu�F �ŕ��т܂��B
(3) (2)�ɂ����āA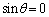 �܂���
�܂���  �C�܂�A
�C�܂�A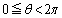 �ɂ����Ă�
�ɂ����Ă� �̂Ƃ��A
�̂Ƃ��A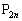 (
(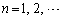 )���ǂ��Ȃ邩�ׂ܂��B(1)(ii)��p���āA
)���ǂ��Ȃ邩�ׂ܂��B(1)(ii)��p���āA �E �̂Ƃ��A
�̂Ƃ��A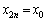 �C
�C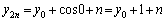 �ƂȂ�A
�ƂȂ�A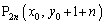 �́A����
�́A����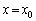 ��ɕ��т܂�(���̂Ƃ����A�D�́A
��ɕ��т܂�(���̂Ƃ����A�D�́A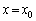 �ƂȂ�̂ŁA(2)�����藧���Ă��܂�)�B
�ƂȂ�̂ŁA(2)�����藧���Ă��܂�)�B �E �̂Ƃ��A
�̂Ƃ��A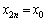 �C
�C �ŁA
�ŁA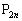 �͂��ׂ�
�͂��ׂ� �ƂȂ�܂��B�D�͒�����\���Ȃ��Ȃ�܂��B
�ƂȂ�܂��B�D�͒�����\���Ȃ��Ȃ�܂��B  ���Ƃ���ƁA�D�́A
���Ƃ���ƁA�D�́A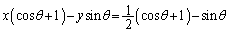 �@����E
�@����E���ׂĂ̓_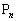 (
( )��1�̒�����ɕ��Ԃ̂ŁA���Ȃ��Ƃ��A
)��1�̒�����ɕ��Ԃ̂ŁA���Ȃ��Ƃ��A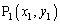 �́A�E��ɂ���܂��B(1)(i)�̌��ʂ�p���āA
�́A�E��ɂ���܂��B(1)(i)�̌��ʂ�p���āA 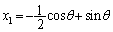 �C
�C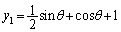
������A�E��x�Cy�ɑ������ƁA
�������āA
�� 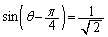
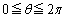 �ɂ����ẮA
�ɂ����ẮA ���A
���A
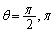 ���������݂������ǂ����A�m�F���܂��B
���������݂������ǂ����A�m�F���܂��B (i) 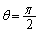 �̂Ƃ��A�E�́A
�̂Ƃ��A�E�́A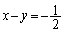 �@����F
�@����F n�������̂Ƃ��́A(2)���A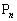 ���F��Ɉʒu���邱�Ƃ͂킩���Ă��܂��Bn����̂Ƃ��A(1)(i)���A
���F��Ɉʒu���邱�Ƃ͂킩���Ă��܂��Bn����̂Ƃ��A(1)(i)���A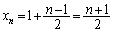 �C
�C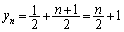
������F��x�Cy�ɑ������Ɛ��藧�̂ŁA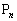 �͇F��̓_�ł��B
�͇F��̓_�ł��B
�]���āA���ׂĂ̓_ (
(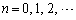 )��1�̒�����ɕ��т܂��B
)��1�̒�����ɕ��т܂��B (ii)  �̂Ƃ��A�E��������\���Ȃ��Ȃ�܂�(����
�̂Ƃ��A�E��������\���Ȃ��Ȃ�܂�(����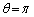 �́A�_�E��ɕ��ԁu�K�v�����v�ł͂Ȃ�)���A
�́A�_�E��ɕ��ԁu�K�v�����v�ł͂Ȃ�)���A n�������̂Ƃ��A��L���A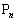 �͂��ׂ�
�͂��ׂ� �ł��Bn����̂Ƃ��A(1)(i)���A
�ł��Bn����̂Ƃ��A(1)(i)���A �C
�C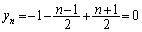
�ƂȂ�A���ׂĂ̓_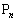 (
( )���A����
)���A����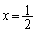 ��ɕ��Ԃ̂ŁA�����ɓK���܂��B
��ɕ��Ԃ̂ŁA�����ɓK���܂��B ����āA ......[��]���D�{���́A�g
......[��]���D�{���́A�g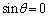 ����
���� 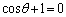 �h�̏ꍇ�A�܂�A
�h�̏ꍇ�A�܂�A �̏ꍇ�́A�ʂɌ�������ׂ��ł����A���������K�v�����ł��邩�̂悤�ɏo�Ă��Ă��܂��̂ŁA�����ɓK���邱�Ƃ��m�F���Ă�����OK�ł��B������ł܂Ƃ߂���邩�A�Ƃ������Ƃ͂���܂����A�_���I�ɂ�����Ɛ����������m�肽���A�����Г�����萳�������Ē����Ƃ悢�Ǝv���܂��B
�̏ꍇ�́A�ʂɌ�������ׂ��ł����A���������K�v�����ł��邩�̂悤�ɏo�Ă��Ă��܂��̂ŁA�����ɓK���邱�Ƃ��m�F���Ă�����OK�ł��B������ł܂Ƃ߂���邩�A�Ƃ������Ƃ͂���܂����A�_���I�ɂ�����Ɛ����������m�肽���A�����Г�����萳�������Ē����Ƃ悢�Ǝv���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 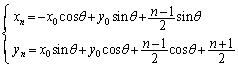 ......[��]
......[��]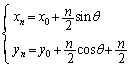 ......[��]
......[��]