���嗝�H���w'09�N[2]
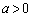 �ɑ��A�s��A��
�ɑ��A�s��A��
�Œ�߂�Bxy���ʏ�̒���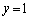 ��
��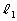 �Ƃ���B
�Ƃ���B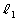 �̊e�_���s��A�ŕ\�����1���ϊ��ňڂ��Ăł��钼����
�̊e�_���s��A�ŕ\�����1���ϊ��ňڂ��Ăł��钼����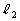 �Ƃ��A
�Ƃ��A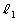 �̊e�_��A�̋t�s��
�̊e�_��A�̋t�s��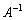 �ŕ\�����1���ϊ��ňڂ��Ăł��钼����
�ŕ\�����1���ϊ��ňڂ��Ăł��钼����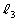 �Ƃ���B�܂��A
�Ƃ���B�܂��A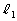 ��
��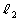 �̌�_��P�C
�̌�_��P�C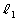 ��
��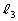 �̌�_��Q�C
�̌�_��Q�C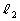 ��
��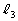 �̌�_��R�Ƃ��A��PQR�̖ʐς�
�̌�_��R�Ƃ��A��PQR�̖ʐς�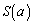 �Ƃ���B�ȉ��̖₢�ɓ�����B
�Ƃ���B�ȉ��̖₢�ɓ�����B
(1) ����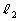 �ƒ���
�ƒ���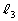 �̕����������߂�B
�̕����������߂�B (2) 3�_P�CQ�CR�̍��W�����߂�B
(3) 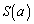 �����߂�B
�����߂�B (4) 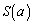 ���ŏ��ɂ���a�����߂�B
���ŏ��ɂ���a�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�P�Ȃ�v�Z���ł��B
(1) ����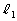 �F
�F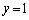 ��̓_
��̓_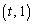 �́AA�ŕ\�����1���ϊ��ɂ���āA
�́AA�ŕ\�����1���ϊ��ɂ���āA ���A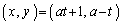 �Ɉڂ�܂��B
�Ɉڂ�܂��B 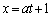 �C
�C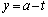
��2�����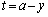 �C������1����������ƁA
�C������1����������ƁA ����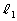 �F
�F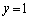 ��̓_
��̓_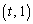 �́A
�́A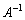 �ŕ\�����1���ϊ��ɂ���āA
�ŕ\�����1���ϊ��ɂ���āA ���A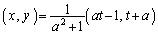 �Ɉڂ�܂��B
�Ɉڂ�܂��B 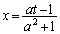 �C
�C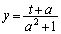
��2�����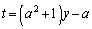 �C������1����������ƁA
�C������1����������ƁA
(2) �@��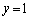 ��������ƁA
��������ƁA �� 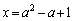
P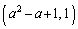 ......[��]
......[��] �A��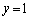 ��������ƁA
��������ƁA �� 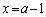
Q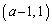 ......[��]
......[��] �@�C�A��A�����ĉ����ƁA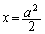 �C
�C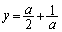
R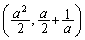 ......[��]
......[��]
(3) ��PQR�̒��PQ�̒����́A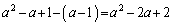 (
(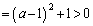 )
) ��PQR�̍����́A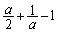 (
(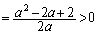 )��
)�� 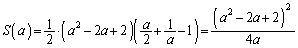 ......[��]
......[��]
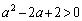 ���A
���A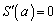 �Ƃ���ƁA
�Ƃ���ƁA�� 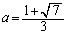 (
(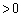 )
)
�����\���A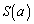 ���ŏ��ɂ���a�́A
���ŏ��ɂ���a�́A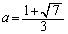 ......[��]�@(���̑������Q��)
......[��]�@(���̑������Q��)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B