早大理工数学'09年[3]
トランプのハートとスペードの1から10までのカードが1枚ずつ総計20枚ある。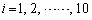
に対して、番号i のハートとスペードのカードの組を第i 対と呼ぶことにする。20枚のカードの中から4枚のカードを無作為に取り出す。取り出された4枚のカードの中に第i 対が含まれているという事象を
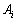で表すとき、以下の問いに答えよ。
(1) 事象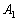
が起こる確率
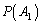を求めよ。 (2) 確率
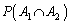を求めよ。 (3) 確率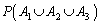
を求めよ。 (4) 取り出された4枚のカードの中に第1対，第2対，第3対，第4対，第5対，第6対の中の少なくとも1つが含まれる確率を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 早大理工の確率の問題としては易しい気がしますが、(4)は論述するとなると、書きにくいかも知れません。
全事象は20枚のカードから4枚のカードを選び出す組み合わせの数で、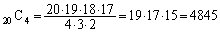
通りあって、どの1通りも等確率で起こります。
(1) 事象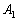
は、4枚のカードを取り出すとき、ハートの1とスペードの1の2枚以外の2枚の選び方を、残る18枚から2枚を選び出す組み合わせの数と考えて、
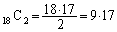通りあります。よって、 
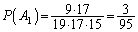......[答]
(2) 事象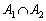
は、ハートの1，2とスペードの1，2の4枚を選び出す事象で、1通り。よって、
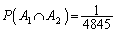......[答]
(3) (1)と同様にして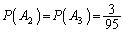
(2)と同様にして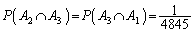
20枚から選び出した4枚の中に、ハートの1，2，3とスペードの1，2，3の6枚がすべて入るということは起こり得ないので、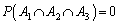
(4) (3)と同様に考えると、20枚から選び出した4枚の中に、3つ以上の対が含まれることは起こり得ないので、事象の集合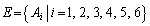
の中から3つを選び出して共通部分を考えたときの確率、Eから4つを選び出して共通部分を考えたときの確率、Eから5つを選び出して共通部分を考えたときの確率、Eから6つすべてを選んで共通部分を考えたときの確率は、いずれも0です。 Eから2つを選び出して(選び方は、6つから2つを選ぶので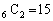
通り)共通部分を考えたときの確率は、(2)と同様にして
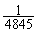です。Eから1つを選び出した(選び方は6通り)ときの確率は、(1)と同様にして
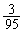です。
よって、4枚のカードの中に第1対，第2対，第3対，第4対，第5対，第6対の中の少なくとも1つが含まれる確率は、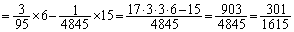 
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
