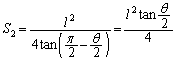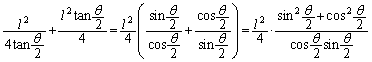���嗝�H���w'09�N[4]
�ȉ��̖₢�ɓ�����B
(1) ���ar�̉~�ɓ��ڂ��A1�̑Ίp���̒�����l�ł���悤�Ȏl�p�`�̖ʐς̍ő�l��r��l�ŕ\���B
(2) ���ar�̉~�ɓ��ڂ���l�p�`�̖ʐς̍ő�l�����߂�B
(3) ��ԓ��̓_O�_�Ƃ��A�l�p�`ABCD���ʂƂ���l�p��(����)��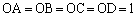 �����Ă���Ƃ���B���̂悤�Ȏl�p���̑̐ς̍ő�l�����߂�B
�����Ă���Ƃ���B���̂悤�Ȏl�p���̑̐ς̍ő�l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��ӂ��Ƃ��A���_�ւ̓��͌����Ă��܂����A�_�q����ƂȂ�Ɩ����m��܂���B
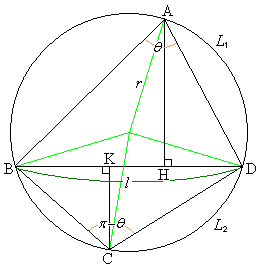 (1) ���ar�̉~�ɓ��ڂ���l�p�`��4���_��A�CB�CC�CD�Ƃ��A������l�ł���Ίp����BD�C
(1) ���ar�̉~�ɓ��ڂ���l�p�`��4���_��A�CB�CC�CD�Ƃ��A������l�ł���Ίp����BD�C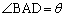 �Ƃ��܂��B
�Ƃ��܂��B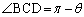 �ł��B
�ł��BB�CD��[�_�Ƃ���2�̉~�ʂ̂����AA������~�ʂ�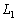 �CC������~�ʂ�
�CC������~�ʂ�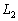 �Ƃ��܂��B
�Ƃ��܂��B
����ʂ̏�ɗ��~���p�͓������̂ŁAA��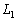 ���B�CD�ȊO�̂ǂ��ɂ��Ă�
���B�CD�ȊO�̂ǂ��ɂ��Ă�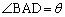 �ł���AC��
�ł���AC��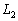 ���B�CD�ȊO�̂ǂ��ɂ��Ă�
���B�CD�ȊO�̂ǂ��ɂ��Ă�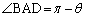 �ł��B�����藝���A
�ł��B�����藝���A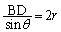
�� 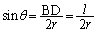 �@����@A����BD�ɉ��낵�������̑���H�CC����BD�ɉ��낵�������̑���K�Ƃ���ƁA
�@����@A����BD�ɉ��낵�������̑���H�CC����BD�ɉ��낵�������̑���K�Ƃ���ƁA
�O�p�`BAD�̖ʐ�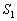 �́A
�́A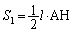
�O�p�`BCD�̖ʐ�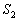 �́A
�́A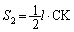 A��
A��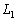 ����Ƃ��AAH�́AAH��
����Ƃ��AAH�́AAH��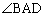 ��2��������Ƃ��ɍő�ŁA���̂Ƃ�
��2��������Ƃ��ɍő�ŁA���̂Ƃ�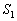 ���ő�ɂȂ�܂��B���̂Ƃ��A
���ő�ɂȂ�܂��B���̂Ƃ��A �ł���A
�ł���A ���l�ɁAC�� ����Ƃ��A
����Ƃ��A �́ACK��
�́ACK��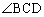 ��2��������Ƃ��ɍő�ɂȂ�܂��B���̂Ƃ��A
��2��������Ƃ��ɍő�ɂȂ�܂��B���̂Ƃ��A �ł���A
�ł���A �]���āA�l�p�`ABCD�̖ʐς̍ő�l�́A
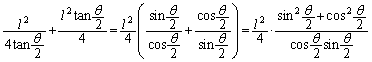
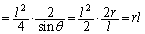 ......[��]�@(�� �@)
......[��]�@(�� �@)�ʉ��D��L�ŁAAH�CCK���ő�ɂȂ�Ƃ��ɂ́AH��K�͓���̓_�ŁAAC�͒��a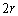 �ɂȂ�܂��B���̂Ƃ��̎l�p�`ABCD�̖ʐς́A
�ɂȂ�܂��B���̂Ƃ��̎l�p�`ABCD�̖ʐς́A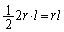
(2) 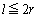 (�����́A�l�p�`ABCD�������`�̂Ƃ��ɐ���)�Ȃ̂ŁA(1)�̌��ʂ��A
(�����́A�l�p�`ABCD�������`�̂Ƃ��ɐ���)�Ȃ̂ŁA(1)�̌��ʂ��A ���ar�̉~�ɓ��ڂ���l�p�`�̖ʐς̍ő�l�́A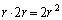 ......[��]
......[��]
(3) 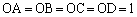 �Ȃ̂ŁAA�CB�CC�CD�́AO�𒆐S�Ƃ��锼�a1�̋��ʏ�̓_�ł��B�l�p�`ABCD���܂ޕ��ʂł��̋����ƁA����͉~�ɂȂ�܂����AA�CB�CC�CD�͂��̉~�̎���Ɉʒu����̂ŁA�l�p�`ABCD�͉~�ɓ��ڂ���l�p�`�ł��B����̉~�̔��a��r�Ƃ���A
�Ȃ̂ŁAA�CB�CC�CD�́AO�𒆐S�Ƃ��锼�a1�̋��ʏ�̓_�ł��B�l�p�`ABCD���܂ޕ��ʂł��̋����ƁA����͉~�ɂȂ�܂����AA�CB�CC�CD�͂��̉~�̎���Ɉʒu����̂ŁA�l�p�`ABCD�͉~�ɓ��ڂ���l�p�`�ł��B����̉~�̔��a��r�Ƃ���A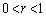 �ł����āA���͈̔͂�1��r�̒l�ɑ��āA(2)���A��ʂ̎l�p�`ABCD�̖ʐς̍ő�l��
�ł����āA���͈̔͂�1��r�̒l�ɑ��āA(2)���A��ʂ̎l�p�`ABCD�̖ʐς̍ő�l��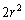 �C���̒��SO�Ǝl�p�`ABCD�Ƃ̋����͎O�����̒藝���
�C���̒��SO�Ǝl�p�`ABCD�Ƃ̋����͎O�����̒藝���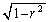 �ł��B���ꂪ�A�l�p���̍����ɂȂ�܂��B
�ł��B���ꂪ�A�l�p���̍����ɂȂ�܂��B ����āA��ʐς��ő�Ƃ���l�p���̑̐�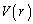 �́A
�́A �����\(���̑������Q��)���A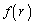 �̍ő�l�F
�̍ő�l�F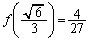
�̐�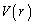 �̍ő�l�F
�̍ő�l�F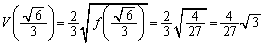 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B