���嗝�H���w'12�N[2]
������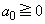 �Ƃ��A�ȉ��̑Q�����Œ�܂鐔��
�Ƃ��A�ȉ��̑Q�����Œ�܂鐔��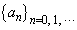 ���l����B
���l����B
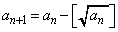 �@(
�@(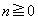 )
)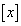 ��x���z���Ȃ��ő�̐�����\���B���̖₢�ɓ�����B
��x���z���Ȃ��ő�̐�����\���B���̖₢�ɓ�����B
(1) 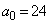 �Ƃ���B���̂Ƃ��A
�Ƃ���B���̂Ƃ��A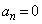 �ƂȂ�ŏ���n�����߂�B
�ƂȂ�ŏ���n�����߂�B (2) m��2�ȏ�̐����Ƃ��A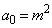 �Ƃ���B���̂Ƃ��A
�Ƃ���B���̂Ƃ��A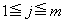 ���݂���j�ɑ���
���݂���j�ɑ���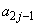 �C
�C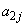 ��j��m�ŕ\���B
��j��m�ŕ\���B (3) m��2�ȏ�̐����Ap��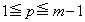 ���݂��������Ƃ��A
���݂��������Ƃ��A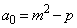 �Ƃ���B���̂Ƃ��A
�Ƃ���B���̂Ƃ��A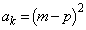 �ƂȂ�k�����߂�B����ɁA
�ƂȂ�k�����߂�B����ɁA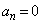 �ƂȂ�ŏ���n�����߂�B
�ƂȂ�ŏ���n�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Q�����̖��ł����A�Q�����̒m����K�v�Ƃ��Ȃ����ł��B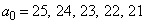 �ȂǂƂ��āA
�ȂǂƂ��āA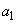 �C
�C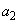 �C��� �����߂Ă����A���ʂ������Ă���̂ł����A(3)���Ȃ��Ȃ����܂��������ł�����J�������܂��B
�C��� �����߂Ă����A���ʂ������Ă���̂ł����A(3)���Ȃ��Ȃ����܂��������ł�����J�������܂��B
(1) 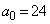 �̂Ƃ��A
�̂Ƃ��A ����āA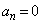 �ƂȂ�ŏ���n�́A
�ƂȂ�ŏ���n�́A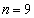 ......[��]
......[��]
(2) 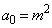 �̂Ƃ��A
�̂Ƃ��A 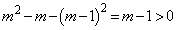 (
(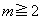 )�C
)�C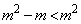 ���A
���A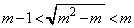 �C
�C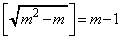
�� 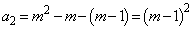
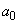 ����
����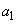 �C
�C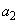 �����߂�Ƃ��Ɠ��l�ɂ��āA
�����߂�Ƃ��Ɠ��l�ɂ��āA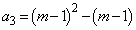 �C
�C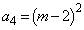
������A
�Ɨ\���ł��܂��B�ȉ��A���w�I�A�[�@�ɂ��A�\�����������邱�Ƃ������܂��B (�T) 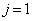 �̂Ƃ��A
�̂Ƃ��A 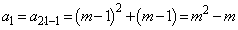 �C
�C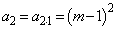
���A�\���͐��藧���܂��B
(�U) 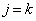 (
(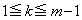 )�̂Ƃ��A�\�������藧�Ɖ��肷��ƁA
)�̂Ƃ��A�\�������藧�Ɖ��肷��ƁA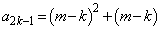 �C
�C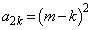 �ƂȂ�܂��B
�ƂȂ�܂��B ����āA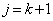 (
(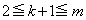 )�̂Ƃ����\���͐������܂��B
)�̂Ƃ����\���͐������܂��B (�T)�C(�U)���A�\���́A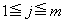 ����j�ɂ��Đ������܂��B����āA
����j�ɂ��Đ������܂��B����āA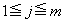 ����j�ɂ���
����j�ɂ��� 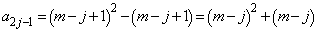
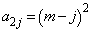 ......[��]
......[��]
(3) (2)�܂łƓ��l�ɂ��Đ���̊e�����v�Z���Ă݂�ƁA
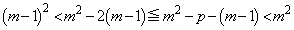 ���A
���A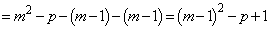 �@����@
�@����@�ƂȂ�A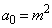 �Ƃ����Ƃ���
�Ƃ����Ƃ���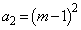 �Ɣ�ׂ�ƁA
�Ɣ�ׂ�ƁA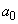 ���m�̍�p���A
���m�̍�p���A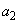 ���m�̍��ł�
���m�̍��ł�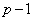 �ɂȂ�A1�������Ȃ�܂��B���̂܂܁A
�ɂȂ�A1�������Ȃ�܂��B���̂܂܁A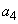 �C����C
�C����C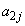 �Ƒ����Ă����ƁA���̍���1���������Ȃ�A
�Ƒ����Ă����ƁA���̍���1���������Ȃ�A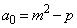 �Ƃ����Ƃ���
�Ƃ����Ƃ���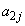 ���A
���A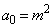 �Ƃ����Ƃ���
�Ƃ����Ƃ���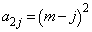 �ɋ߂Â��čs�������ł��B�@�Ɠ��l�ɂ��āA���ہA
�ɋ߂Â��čs�������ł��B�@�Ɠ��l�ɂ��āA���ہA �E�E�E�E�E�E
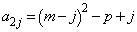 �@����A
�@����A�ƂȂ�̂ŁA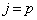 �ƂȂ����Ƃ��A
�ƂȂ����Ƃ��A 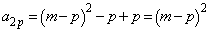 �@����B
�@����B�ƂȂ�܂��B����āA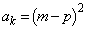 �ƂȂ�k�́A
�ƂȂ�k�́A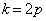 ......[��]
......[��]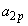 �Ȍ�̍��ɂ��ẮA(2)�Ɠ��l�ɁA
�Ȍ�̍��ɂ��ẮA(2)�Ɠ��l�ɁA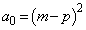 �Ƃ����ꍇ���l����ƁA
�Ƃ����ꍇ���l����ƁA �ƂȂ�܂��B�]���āA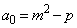 �̂Ƃ��ɂ́A�B���A
�̂Ƃ��ɂ́A�B���A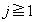 �Ƃ��āA
�Ƃ��āA 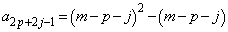 �@����C
�@����C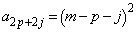
�ƂȂ�܂��B�A���A����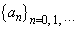 �̊e���́A��n����
�̊e���́A��n����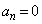 �ɂȂ��Ă��܂��ƁA
�ɂȂ��Ă��܂��ƁA �ƂȂ�A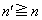 �ƂȂ�S�Ă̑�
�ƂȂ�S�Ă̑�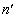 ����
����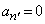 �ƂȂ��Ă��܂��A�C���Ӗ��������Ȃ��Ȃ�܂��B�C���Ӗ������̂́A
�ƂȂ��Ă��܂��A�C���Ӗ��������Ȃ��Ȃ�܂��B�C���Ӗ������̂́A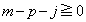 �C�܂�A(
�C�܂�A(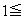 )
)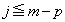 �̂Ƃ��ł��B
�̂Ƃ��ł��B
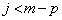 �ɂ����ẮA
�ɂ����ẮA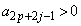 �C
�C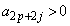 �ł����A
�ł����A
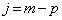 �̂Ƃ��A
�̂Ƃ��A �ƂȂ�܂��B������A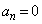 �ƂȂ�ŏ���n�́A
�ƂȂ�ŏ���n�́A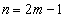 ......[��]
......[��] ���D�A�ŁA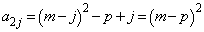 �Ƃ���ƁA
�Ƃ���ƁA 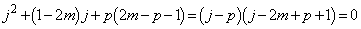 ��
�� 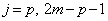 �ƂȂ�A
�ƂȂ�A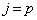 �ȊO�ɁA
�ȊO�ɁA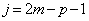 �Ƃ����ꍇ���o�Ă���̂ł����A
�Ƃ����ꍇ���o�Ă���̂ł����A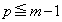 �Ȃ̂ŁA
�Ȃ̂ŁA
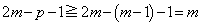 �@(�����́A
�@(�����́A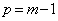 �̂Ƃ�)�ƂȂ�A
�̂Ƃ�)�ƂȂ�A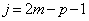 �́A
�́A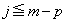 �Ƃ������������܂���B
�Ƃ������������܂���B
�܂��A�C�ŁA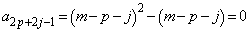 �Ƃ���ƁA
�Ƃ���ƁA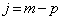 �̑��ɁA
�̑��ɁA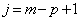 �Ƃ����ꍇ���o�Ă��܂����A��͂�A
�Ƃ����ꍇ���o�Ă��܂����A��͂�A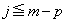 �Ƃ������������܂���B
�Ƃ������������܂���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B