早稲田大学基幹・創造・先進理工学部2012年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 以下の問いに答えよ。
(1) 複素数α，β に対して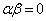
ならば、
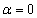または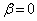
であることを示せ。 (2) 複素数αに対して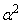
が正の実数ならば、αは実数であることを示せ。 (3) 複素数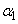
，
，･･･，
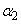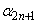(nは自然数)に対して、
，･･･，
，･･･，
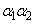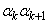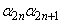および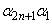
がすべて正の実数であるとする。このとき、
，
，･･･，
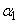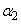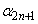はすべて実数であることを示せ。 [解答へ]
[2] 初項を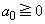
とし、以下の漸化式で定まる数列
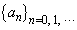を考える。
(
)
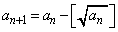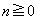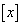はxを越えない最大の整数を表す。次の問いに答えよ。
(1) 
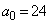とする。このとき、
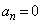となる最小のnを求めよ。 (2) mを2以上の整数とし、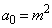
とする。このとき、
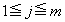をみたすjに対して
，
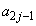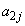をjとmで表せ。 (3) mを2以上の整数、pを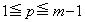
をみたす整数とし、
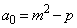とする。このとき、
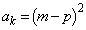となるkを求めよ。さらに、
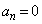となる最小のnを求めよ。 [解答へ]
[3] 表が出る確率がa (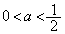
)，裏が出る確率が
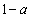のコインを1枚投げる試行をn回行う。ただし
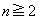とする。このn回の試行の結果、表が2回以上出る事象を
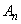で表す。また1回目からn回目の試行が終わるまでに、「裏→表」の順で出ない事象を
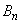で表す。次の問いに答えよ。
(1) 確率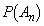
，
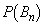を求めよ。 (2) 確率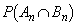
を求めよ。 (3) 極限
を求めよ。ただし、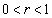
をみたすrに対して、
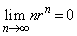となることを証明なしに用いてよい。 [解答へ]
[4] 関数
(
)
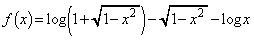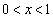(1) 
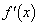を求めよ。 (2)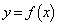 
のグラフの概形を描け。 (3) 曲線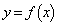
上を動く点をPとする。点Qは、曲線
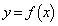のPにおける接線上にあり、Pとの距離が1で、そのx座標がPのx座標より小さいものとする。Qの軌跡を求めよ。 [解答へ]
[5] xy平面上に2点A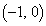
，B
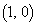をとる。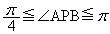
をみたす平面上の点Pの全体と点A，Bからなる図形をFとする。次の問いに答えよ。
(1) Fを図示せよ。
(2) Fをx軸のまわりに1回転して得られる立体の体積を求めよ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 