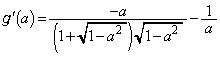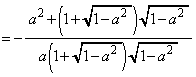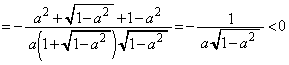早大理工数学'12年[4]
関数
(
)
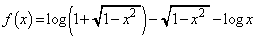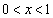(1) 
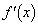を求めよ。 (2) 
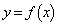のグラフの概形を描け。 (3) 曲線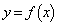
上を動く点をPとする。点Qは、曲線
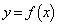のPにおける接線上にあり、Pとの距離が1で、そのx座標がPのx座標より小さいものとする。Qの軌跡を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 問題文の式だけ見ると、膝がガクガク震えそうですが、題材は、早大理工'96年[5]でも取り上げられている「追跡線」と呼ばれる関数です。やってみると意外と大したことはありません。昨年の東大理系前期[3]の積分の問題にも類似の関数が登場します。
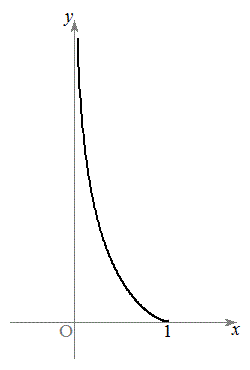(2) (1)より、
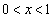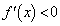において
で、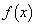
は減少関数です。
，
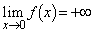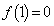より、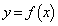
のグラフの概形は右図。
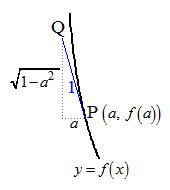(3) 点Pのx座標を
(
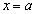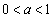)とすると、y座標は
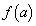です。点Pにおける接線の傾きは、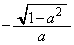
Qのx座標がPのx座標より小さいことと、PQの長さが1であることから、右図より、点Qのx座標は、 y座標は、
(
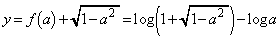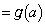とおきます)(1)と同様にして、
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。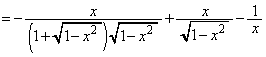 
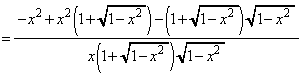
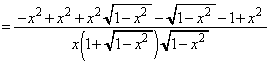
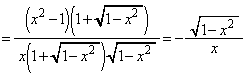......[答]
は
において減少関数で、
，
より、
の部分