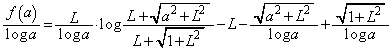���嗝�n���w'11�N�O��[3]
L�𐳒萔�Ƃ���B���W���ʂ�x����̐��̕����ɂ���_P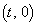 �ɑ��A���_O�𒆐S�Ƃ��_P��ʂ�~������AP����o�����Ĕ����v���ɓ��̂�L�����i�_��Q
�ɑ��A���_O�𒆐S�Ƃ��_P��ʂ�~������AP����o�����Ĕ����v���ɓ��̂�L�����i�_��Q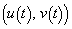 �ƕ\���B
�ƕ\���B
(1) 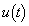 �C
�C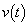 �����߂�B
�����߂�B (2) 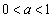 �͈̔͂̎���a�ɑ��A�ϕ�
�͈̔͂̎���a�ɑ��A�ϕ� �����߂�B
(3) �Ɍ�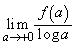 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ϕ��̌v�Z���ł��B������Ȃ��`�ł����u���ϕ��ɂ������ł��܂��B
(1) ���_�𒆐S�Ƃ��_P��ʂ�~���̔��a��t �ł��B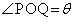 �Ƃ���ƁA��PQ�̒�����L���A
�Ƃ���ƁA��PQ�̒�����L���A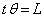 �@(��ʊp���Q��)
�@(��ʊp���Q��) �� 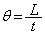 ������A
������A 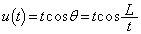 �C
�C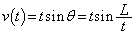 ......[��]
......[��]
�Ƃ��āA���F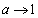 �̂Ƃ��Aθ�F
�̂Ƃ��Aθ�F
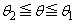 �ɂ�����
�ɂ�����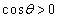 �C
�C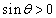
�� 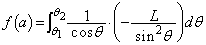
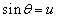 �Ƃ����ƁA
�Ƃ����ƁA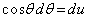 �Cθ�F
�Cθ�F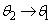 �̂Ƃ�u�F
�̂Ƃ�u�F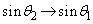
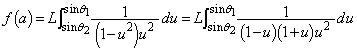
��ϕ����������ɕ����܂�(�������̐ϕ����Q��)�B�Ƃ����ƁA���̉E�ӂ�ό`���āA
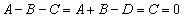 �C
�C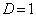
�� 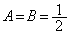 ��
�� 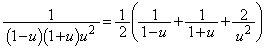
�����ŁA�@���g����悤�ɕό`���܂��B
����āA
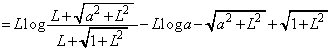 ......[��]
......[��]
(3) 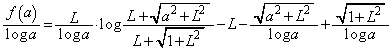
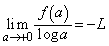 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 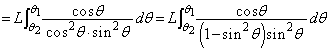
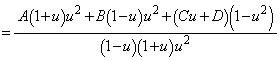
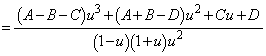
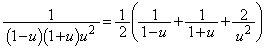
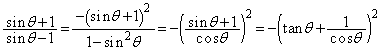
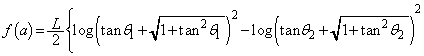
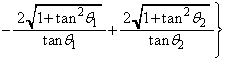
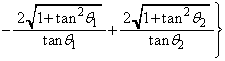
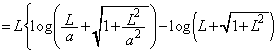
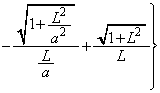
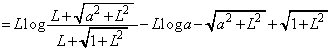 ......[��]
......[��]