早大理工数学'12年[1]
以下の問いに答えよ。
(1) 複素数α，β に対して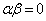
ならば、
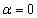または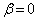
であることを示せ。 (2) 複素数αに対して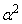
が正の実数ならば、αは実数であることを示せ。 (3) 複素数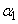
，
，･･･，
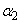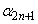(nは自然数)に対して、
，･･･，
，･･･，
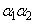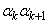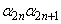および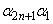
がすべて正の実数であるとする。このとき、
，
，･･･，
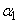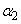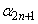はすべて実数であることを示せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 現過程では意表を突く問題と言えないこともありませんが、かつて複素数平面が入試範囲だった頃であれば易問です。
以下、iを虚数単位(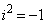
)とします。
(1) p，q，r，sを実数として、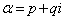
，
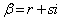とします。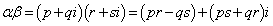 
(複素数の計算を参照)
⇔ 
⇔ 
⇔ 
⇔ 
⇔ 
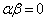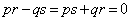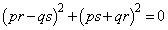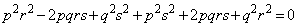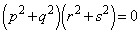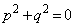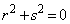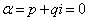または 
⇔ 
または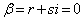 
別解．上記と実質的に同じですが、絶対値を用いれば以下のように書けます。
(2) p，qを実数として、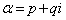
とします。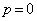 
だとすると、
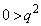を満たす実数qが存在しないので、
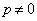，つまり、
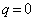です。
よって、αは実数です。別解．複素数αの偏角を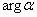
(
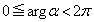)と表すと、
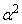の偏角は、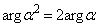
(偏角argにはlogのような性質があります)です。
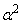が正の実数だとすると、
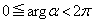として、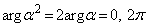 
∴ 
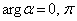
よって、αは実数です。
(3) 
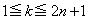となる、ある整数kに対して、
，
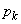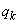を実数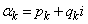として、
として、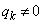
と仮定します。 
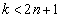のときは、これが、正の実数であるとき、
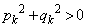より、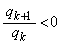
つまり、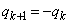
同様に、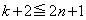
であれば、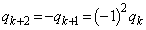
また、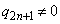
であれば、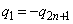
これより、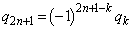
∴ 
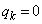
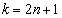だとしても、
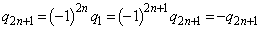となるので、
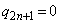となります。
いずれにしても、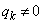
とした仮定と矛盾します。よって、仮定は誤りで、
，
，･･･，
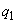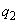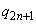はいずれも0であって、
，
，･･･，
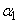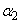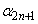はすべて実数です。 別解．上記と実質的に同じですが、偏角を用いて以下のように解答することができます。
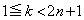である整数kに対して、
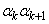が正の実数であることから、
(
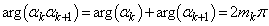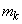は整数)
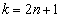のときは、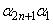
が正の実数であることから、
(
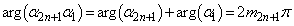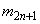は整数)これより、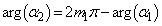
・・・・・・
∴ 
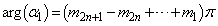よって、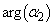
，･･･，
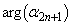はすべてπの整数倍となり、
，
，･･･，
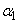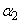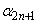は実数です。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
⇔ 
⇔ 
または 
または 
は正の実数 ⇔ 
かつ 
かつ 
