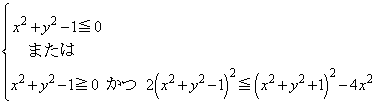���嗝�H���w'12�N[5]
xy���ʏ��2�_A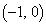 �CB
�CB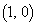 ���Ƃ�B
���Ƃ�B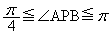 ���݂������ʏ�̓_P�̑S�̂Ɠ_A�CB����Ȃ�}�`��F�Ƃ���B���̖₢�ɓ�����B
���݂������ʏ�̓_P�̑S�̂Ɠ_A�CB����Ȃ�}�`��F�Ƃ���B���̖₢�ɓ�����B
(1) F��}������B
(2) F��x���̂܂���1��]���ē����闧�̂̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�̌��ʂ͌����Ă���̂ŁA�_���邱�Ƃ��e�[�}�ł��B
(1) 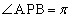 �̂Ƃ��A�_P�̑S�̂͐���AB�ł��B
�̂Ƃ��A�_P�̑S�̂͐���AB�ł��B 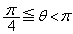 �Ƃ��āA
�Ƃ��āA �̂Ƃ��A�~���p�̒藝���A�_P�̑S�͉̂~�̈ꕔ�ł��B�~��C�Ƃ��܂��B�܂��A�_P��
�̂Ƃ��A�~���p�̒藝���A�_P�̑S�͉̂~�̈ꕔ�ł��B�~��C�Ƃ��܂��B�܂��A�_P��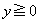 �̕����ɂ���ꍇ���l���܂��B
�̕����ɂ���ꍇ���l���܂��B
���̉~�̔��a��r�C�~�̒��S��D�Ƃ���ƁA�Ώ̐�����D��y����̓_(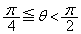 �̂Ƃ��ɂ�
�̂Ƃ��ɂ�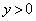 �̕����ɂ���A
�̕����ɂ���A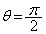 �̂Ƃ��ɂ͌��_O�C
�̂Ƃ��ɂ͌��_O�C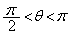 �̂Ƃ��ɂ�
�̂Ƃ��ɂ� �̕����ɂ���܂�)�ł��B
�̕����ɂ���܂�)�ł��B
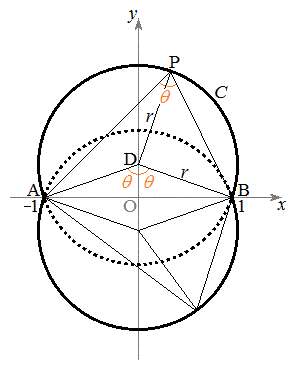 �E�}���A
�E�}���A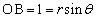 �C
�C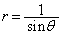 �CD��y���W��
�CD��y���W��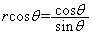 (������
(������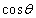 �̐����ƈ�v���܂�)�~C�̕������́A
�̐����ƈ�v���܂�)�~C�̕������́A�~C�́A2�_A�CB��ʂ�̂ŁA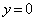 �̂Ƃ��A���R�A
�̂Ƃ��A���R�A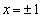 �ł��B
�ł��B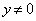 �̂Ƃ��A
�̂Ƃ��A 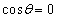 (
(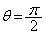 )�̏ꍇ�������āA
)�̏ꍇ�������āA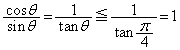 �C
�C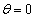 �̏ꍇ���܂߂�
�̏ꍇ���܂߂�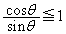 ���A
���A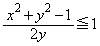
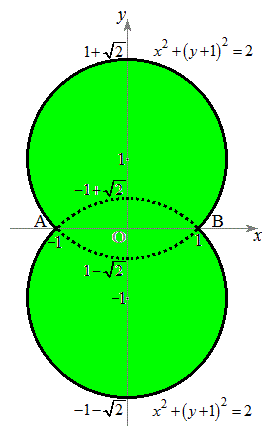 �ȏ���A
�ȏ���A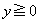 �̂Ƃ��A
�̂Ƃ��A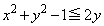 �@��
�@�� 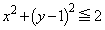 �C�_P�̑S�̂́A
�C�_P�̑S�̂́A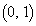 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a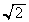 �̉~��������ł��B
�̉~��������ł��B
�_P��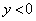 �̕����ɂ���ꍇ�A��L�ŁA�~C�̔��a��
�̕����ɂ���ꍇ�A��L�ŁA�~C�̔��a��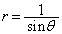 �̂܂܂ł����A���S��y���W��
�̂܂܂ł����A���S��y���W��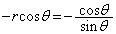 �ƂȂ�A�~C�̕������́A
�ƂȂ�A�~C�̕������́A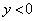 �̂Ƃ��A
�̂Ƃ��A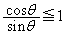 ���A
���A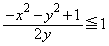 �@��
�@�� 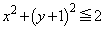 �C�_P�̑S�̂́A
�C�_P�̑S�̂́A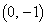 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a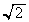 �̉~��������ł��B
�̉~��������ł��B
�ȏ���AF��}������(�s�����̕\���̈����Q��)�ƉE�}���ΐF���F��(���E�����܂�)�B���D���_�͌����Ă���̂ŁA��L��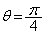 �̂Ƃ��̉~�������l���A
�̂Ƃ��̉~�������l���A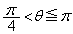 �̂Ƃ��̓_P�͂��̉~�̓����ɗ��邱�Ƃ������A�Ƃ������j���l�����܂��B
�̂Ƃ��̓_P�͂��̉~�̓����ɗ��邱�Ƃ������A�Ƃ������j���l�����܂��B
(2) F��x���Ɋւ��đΏ̂Ȑ}�`�ł��BF��x���̂܂���1��]���ē����闧�̂́AF�̋��E��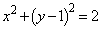 ��x���̂܂���1��]���ē����闧�̂ŁAy�ɂ��ĉ����ƁA
��x���̂܂���1��]���ē����闧�̂ŁAy�ɂ��ĉ����ƁA �ƂȂ邱�Ƃ���A���߂�̐�V�́A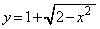 ��
��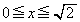 �C
�C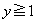 �̕�����x���̂܂���1��]���ē����闧�̂̑̐ς���A
�̕�����x���̂܂���1��]���ē����闧�̂̑̐ς���A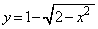 ��
��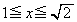 �C
�C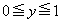 �̕�����x���̂܂���1��]���ē����闧�̂̑̐ς�������2�{�������̂ł�(x���̂܂��̉�]�����Q��)�B
�̕�����x���̂܂���1��]���ē����闧�̂̑̐ς�������2�{�������̂ł�(x���̂܂��̉�]�����Q��)�B
(1)�̕ʉ��D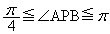 ���݂���xy���ʏ�̓_P�̍��W��
���݂���xy���ʏ�̓_P�̍��W��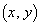 �Ƃ��܂��B
�Ƃ��܂��B 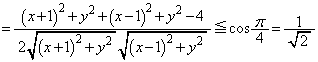 �@(��
�@(�� 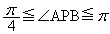 )
)������A
�����ŁA
���A�f���ɓW�J���Ă��܂��ƁA
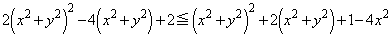
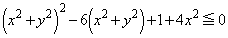 �@����@
�@����@�����ōs���l�܂��Ă��܂��܂��B
���_�͌����Ă���̂ŁA���_�̕�����l���܂��B�_P��F�̋��E���ƂȂ肻����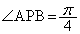 �̂Ƃ��A�~���p�̒藝����A�_P�̑S�͉̂~�̈ꕔ�ƂȂ�܂��B���̉~�́A2�_A�CB��ʂ�̂ŁA���̔��a��
�̂Ƃ��A�~���p�̒藝����A�_P�̑S�͉̂~�̈ꕔ�ƂȂ�܂��B���̉~�́A2�_A�CB��ʂ�̂ŁA���̔��a��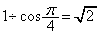 �C���S�́A�_P��x�������ɂ���Ƃ��ɂ�
�C���S�́A�_P��x�������ɂ���Ƃ��ɂ�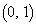 �C�_P��x�����牺�ɂ���Ƃ��ɂ�
�C�_P��x�����牺�ɂ���Ƃ��ɂ�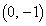 �ŁA�~�̕������́A
�ŁA�~�̕������́A �ƂȂ�A�@�̍��ӂ�������������ƁA
�Ƃ����`���o�Ă��邱�Ƃ��\�z�ł��܂��B�����W�J���Ă݂�ƁA
�ƂȂ��āA�@�̍��ӂɈ�v���܂��B
�]���āA�@���A
����āA
�h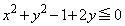 ����
���� 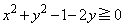 �h
�h �܂��́A
�h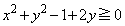 ����
���� 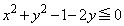 �h
�h ������A�}�`F�́A
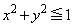 (�~
(�~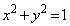 �������)
�������)�܂���
�h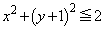 ����
���� 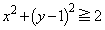 �h (�~
�h (�~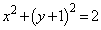 ��������A���A�~
��������A���A�~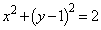 ����O��)
����O��) �܂��́A
�h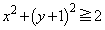 ����
���� 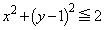 �h (�~
�h (�~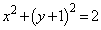 ����O���A���A�~
����O���A���A�~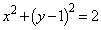 �������)
�������)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 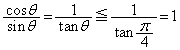 �C
�C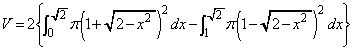
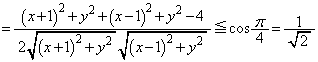 �@(��
�@(��