���嗝�H���w'26�N[2]
k�����R���Ƃ���B������
�������R���̑g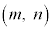 �����R�����ƌĂԁB�ȉ��̖�ɓ�����B
�����R�����ƌĂԁB�ȉ��̖�ɓ�����B
(1) ���R����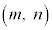 �����݂���Ȃ�A
�����݂���Ȃ�A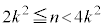 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B (2) ���ꂼ���k�ɑ��āA���R���������Ȃ��Ƃ�1���݂��A���̌���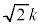 ��菬�������Ƃ������B
��菬�������Ƃ������B (3) 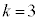 �̂Ƃ��A���R���������ׂċ��߂�B
�̂Ƃ��A���R���������ׂċ��߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@2�d�������O�������F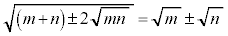 (��������)���l�^�ɂ��������̖��ł��B2�悷��Ƃ��ɁA2�悷����̂̐����̊m�F��Y���ƍs���l��܂��B
(��������)���l�^�ɂ��������̖��ł��B2�悷��Ƃ��ɁA2�悷����̂̐����̊m�F��Y���ƍs���l��܂��B
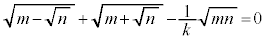 �@����@
�@����@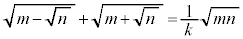
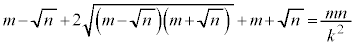
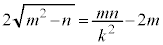 �@����A
�@����A
(1) �����ō��ӂ�0�ȏ�Ȃ̂�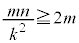 �C�����A���R����
�C�����A���R����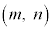 �����݂���Ƃ��A
�����݂���Ƃ��A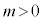 ���
���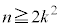 �@����B
�@����B ����ɗ��ӂ�2�悷��ƁA
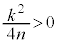 �������āA
�������āA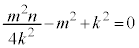
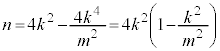 �@����C
�@����C������A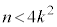 �@����D
�@����D
�B�C�D���A���R����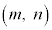 �����݂���Ȃ�A
�����݂���Ȃ�A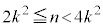
����āA��ӂ͎�����܂����B
(��) �C�ŁA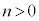 ���A
���A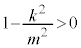 �C�܂��A�B�ƇC���
�C�܂��A�B�ƇC���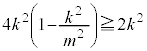 �C
�C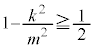
�� 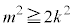 �@����E
�@����E
�܂��C�ɂ����āAn�C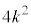 �͎��R���Ȃ̂�
�͎��R���Ȃ̂�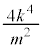 �����R���ł���A
�����R���ł���A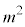 ��
��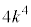 �̖ł����āA
�̖ł����āA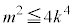 �@����F
�@����F
�E�C�F���A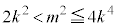 �@����G
�@����G
(2) (1)(��)���A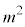 ��
��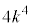 �̖ł����A
�̖ł����A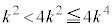 �Ȃ̂ŁA�G�����Ƃ��āA
�Ȃ̂ŁA�G�����Ƃ��āA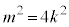 ������܂��B���̂Ƃ��C���A
������܂��B���̂Ƃ��C���A ����n�́A(1)��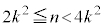 �����Ă��܂��B���R��m��
�����Ă��܂��B���R��m��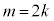 �ƂȂ�܂����A
�ƂȂ�܂����A 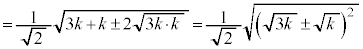
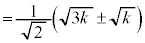 �@(��������)
�@(��������)�@���ӂɑ������ƁA
�ƂȂ�A�@�����̂ŁA���ꂼ���k�ɑ��āA���R����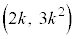 ��1���݂��܂��B(1)(��)���A
��1���݂��܂��B(1)(��)���A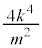 �͎��R���ł��B�G���
�͎��R���ł��B�G���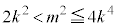 �C
�C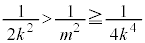 �C����āA
�C����āA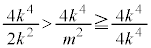
�� 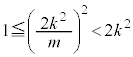 �C
�C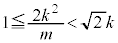 �@����H
�@����H
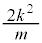 �͗L�����ł����A���R���łȂ��L�����ŁA2�悪�������łȂ����R�����Ƃ���ƁA
�͗L�����ł����A���R���łȂ��L�����ŁA2�悪�������łȂ����R�����Ƃ���ƁA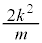 ���������ƂȂ薵������̂ŁA
���������ƂȂ薵������̂ŁA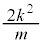 �����R���ł��B���ꂼ���k�ɑ��āA�H�������R����
�����R���ł��B���ꂼ���k�ɑ��āA�H�������R����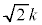 �����ŁA�H����m��
�����ŁA�H����m��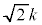 �����ł���Am�����܂�·C�ɂ��n��1�ʂ�Ɍ��܂�̂ŁA���R����
�����ł���Am�����܂�·C�ɂ��n��1�ʂ�Ɍ��܂�̂ŁA���R����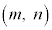 �̌���
�̌���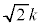 �����������Ȃ�܂��B
�����������Ȃ�܂��B
(3) 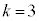 �̂Ƃ��A�C��
�̂Ƃ��A�C��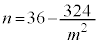 �@����I
�@����I �H��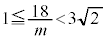 �ƂȂ�܂��B����������R��
�ƂȂ�܂��B����������R��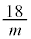 �́A
�́A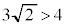 �Ȃ̂�
�Ȃ̂�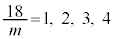 �ł��B���̂���m�����R���ɂȂ�̂́A
�ł��B���̂���m�����R���ɂȂ�̂́A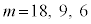
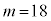 �̂Ƃ��A�I���A
�̂Ƃ��A�I���A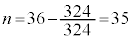
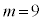 �̂Ƃ��A�I���A
�̂Ƃ��A�I���A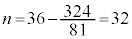
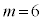 �̂Ƃ��A�I���A
�̂Ƃ��A�I���A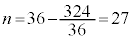 (1)��
(1)��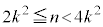 �́A
�́A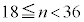 �ƂȂ�܂����A��L3�ʂ�͂�������Ă��܂��B
�ƂȂ�܂����A��L3�ʂ�͂�������Ă��܂��B
����āA���R�����́A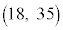 �C
�C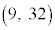 �C
�C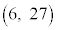 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2026(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 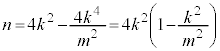 �@����C
�@����C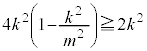 �C
�C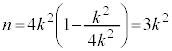
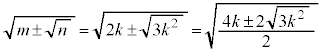
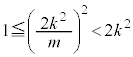 �C
�C