早稲田大学基幹・創造・先進理工学部2026年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 次の関数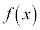 について、以下の問に答えよ。
について、以下の問に答えよ。
(1) 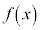 の極大値Mと極小値mを求めよ。
の極大値Mと極小値mを求めよ。 (2) (1)で求めたM,mに対して、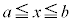 における
における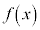 の最大値がM,最小値がmとなるような実数の組
の最大値がM,最小値がmとなるような実数の組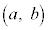 のうち、
のうち、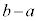 が最小となる組を求めよ。
が最小となる組を求めよ。 [解答へ]
[2] kを自然数とする。方程式
を満たす自然数の組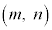 を自然数解と呼ぶ。以下の問に答えよ。
を自然数解と呼ぶ。以下の問に答えよ。
(1) 自然数解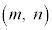 が存在するならば、
が存在するならば、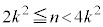 であることを示せ。
であることを示せ。 (2) それぞれのkに対して、自然数解が少なくとも1つ存在し、その個数は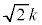 より小さいことを示せ。
より小さいことを示せ。 (3) 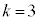 のとき、自然数解をすべて求めよ。
のとき、自然数解をすべて求めよ。 [解答へ]
[3] 座標空間内に点A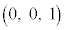 ,B
,B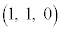 ,および実数aを用いて表される点P
,および実数aを用いて表される点P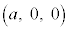 をとる。さらに、2点
をとる。さらに、2点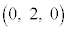 ,
,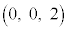 を通る直線を
を通る直線を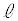 として、3点A,B,Pが定める平面と直線
として、3点A,B,Pが定める平面と直線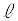 との交点をQとする。
との交点をQとする。
(1) 点Qの座標をaを用いて表せ。
(2) 4点A,B,P,Qが四角形APBQを成し、線分ABと線分PQが交わるためのaの条件を求めよ。
(3) aが(2)の条件を満たすとき、四角形ABPQの面積をaを用いて表せ。
[解答へ]
[4] 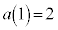 とし、
とし、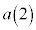 ,
,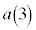 ,
,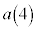 ,・・・を次の関係で定める。
,・・・を次の関係で定める。
以下の問に答えよ。
(1) 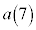 ,
,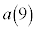 を求めよ。
を求めよ。 (2) 自然数nに対して、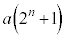 は、1または2のいずれかの値をとるような
は、1または2のいずれかの値をとるような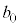 ,
,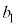 ,・・・,
,・・・,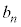 を用いて、
を用いて、 (3) 自然数nに対して、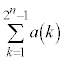 を求めよ。
を求めよ。 [解答へ]
[5] 関数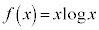 について、以下の問に答えよ。ただし、
について、以下の問に答えよ。ただし、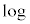 は自然対数、eは自然対数の底を表す。必要ならば、
は自然対数、eは自然対数の底を表す。必要ならば、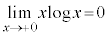 を用いてよい。
を用いてよい。
(1) 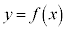 の増減、極値を調べて、そのグラフをかけ。
の増減、極値を調べて、そのグラフをかけ。 (2) 実数aに対して、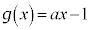 とする。曲線
とする。曲線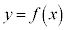 と直線
と直線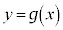 の共有点の個数は、aの値によってどのように変わるか調べよ。
の共有点の個数は、aの値によってどのように変わるか調べよ。 (3) 曲線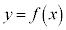 と直線
と直線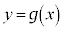 の共有点の個数が1個のとき、曲線
の共有点の個数が1個のとき、曲線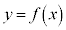 ,直線
,直線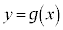 および直線
および直線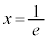 で囲まれた部分をy軸の周りに1回転させてできる立体の体積を求めよ。
で囲まれた部分をy軸の周りに1回転させてできる立体の体積を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。なお、解答は、
苦学楽学塾制作です。©2005-2026(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 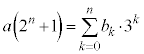
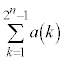 を求めよ。
を求めよ。