���嗝�H���w'26�N[1]
���̊�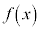 �ɂ��āA�ȉ��̖�ɓ�����B
�ɂ��āA�ȉ��̖�ɓ�����B
(1) 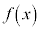 �̋ɑ�lM�Ƌɏ��lm�����߂�B
�̋ɑ�lM�Ƌɏ��lm�����߂�B (2) (1)�ŋ��߂�M�Cm�ɑ��āA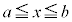 �ɂ�����
�ɂ�����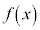 �̍ő�l��M�C�ŏ��l��m�ƂȂ�悤�Ȏ����̑g
�̍ő�l��M�C�ŏ��l��m�ƂȂ�悤�Ȏ����̑g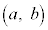 �̂����A
�̂����A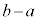 ���ŏ��ƂȂ�g�����߂�B
���ŏ��ƂȂ�g�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(2)�͂Ђ��������ł��B�ɑ�̈ʒu����ɏ��̈ʒu�܂łƁA�����Ɍ��߂��Ȃ��悤�ɒ��ӂ��܂��傤�B3�����ł́A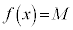 �ƂȂ�̂͋ɑ�̂Ƃ��낾���ł͂���܂���B
�ƂȂ�̂͋ɑ�̂Ƃ��낾���ł͂���܂���B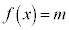 �ƂȂ�̂��ɏ��̂Ƃ��낾���ł͂���܂���B
�ƂȂ�̂��ɏ��̂Ƃ��낾���ł͂���܂���B
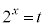 �Ƃ����ƁA
�Ƃ����ƁA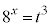 �C
�C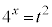 ���A
���A
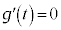 �Ƃ���ƁA
�Ƃ���ƁA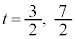
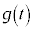 �������\�́A
�������\�́A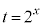 �����������x����������̂ŁA
�����������x����������̂ŁA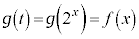 �̑�����
�̑�����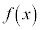 �̑����͈�v���A
�̑����͈�v���A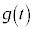 ���ɑ�̂Ƃ�
���ɑ�̂Ƃ�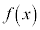 ���ɑ�A
���ɑ�A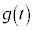 ���ɏ��̂Ƃ�
���ɏ��̂Ƃ�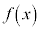 ���ɏ��ł��B
���ɏ��ł��B
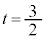 �̂Ƃ��A
�̂Ƃ��A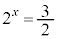 �C
�C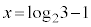
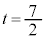 �̂Ƃ��A
�̂Ƃ��A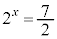 �C
�C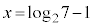
�ɑ�l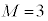 (
(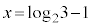 �̂Ƃ�)�C�ɏ��l
�̂Ƃ�)�C�ɏ��l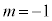 (
(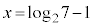 �̂Ƃ�) ......[��]
�̂Ƃ�) ......[��]
(2) 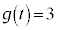 �Ƃ���ƁA�@���A
�Ƃ���ƁA�@���A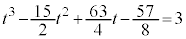
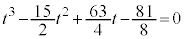 �@����A
�@����A�A�́A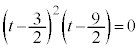 �ƂȂ�܂����A
�ƂȂ�܂����A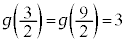 (
(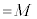 )�ł��B
)�ł��B
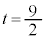 �̂Ƃ��A
�̂Ƃ��A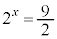 �C
�C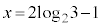 �ł����A
�ł����A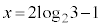 �ɂ�����
�ɂ�����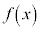 �͑������Ă��܂��B�@����B
�͑������Ă��܂��B�@����B
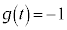 �Ƃ���ƁA�@���A
�Ƃ���ƁA�@���A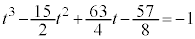
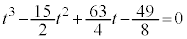 �@����C
�@����C�d��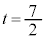 �ȊO�̉���β�Ƃ��āA���ƌW���̊W���A
�ȊO�̉���β�Ƃ��āA���ƌW���̊W���A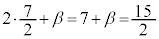 �@��
�@�� 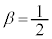 �C�́A
�C�́A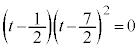 �ƂȂ�܂����A
�ƂȂ�܂����A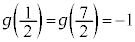 (
(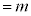 )�ł��B
)�ł��B
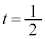 �̂Ƃ��A
�̂Ƃ��A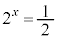 �C
�C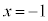 �ł����A
�ł����A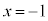 �ɂ�����
�ɂ�����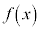 �͑������Ă��܂��B�@����D
�͑������Ă��܂��B�@����D
�ȏ�Ɋ�Â��āA�͈�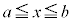 �ɂ�����
�ɂ�����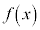 �̍ő�l�A�ŏ��l���l���܂��B(1)�̑����̌��ʂƇB���A
�̍ő�l�A�ŏ��l���l���܂��B(1)�̑����̌��ʂƇB���A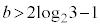 �Ƃ���ƁA�ő�l��M���傫���Ȃ�܂��B(1)�̑����̌��ʂƇD���A
�Ƃ���ƁA�ő�l��M���傫���Ȃ�܂��B(1)�̑����̌��ʂƇD���A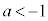 �Ƃ���ƁA�ŏ��l��m��菬�����Ȃ�܂��B
�Ƃ���ƁA�ŏ��l��m��菬�����Ȃ�܂��B
���̓_�ɒ��ӂ���ƁA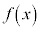 �̍ő�l��M�C�ŏ��l��m�ɂȂ�
�̍ő�l��M�C�ŏ��l��m�ɂȂ�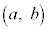 �̑g�́A�͈�
�̑g�́A�͈�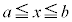 ��
��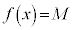 �ƂȂ�x�C
�ƂȂ�x�C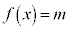 �ƂȂ�x���Ƃ��Ɋ܂ނ��̂Ƃ��āA�ȉ��̏ꍇ���l�����܂��B
�ƂȂ�x���Ƃ��Ɋ܂ނ��̂Ƃ��āA�ȉ��̏ꍇ���l�����܂��B (i) 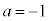 �C
�C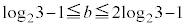
(ii) 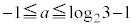 �C
�C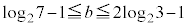
(iii) 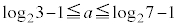 �C
�C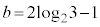
�e�X�̏ꍇ��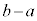 ���ŏ��ɂȂ���̂��l���܂��B
���ŏ��ɂȂ���̂��l���܂��B (i)�ł́A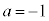 �C
�C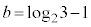 �̂Ƃ��ɁA
�̂Ƃ��ɁA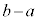 �́A
�́A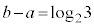 �ƂȂ�ŏ��ł��B
�ƂȂ�ŏ��ł��B (ii)�ł́A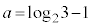 �C
�C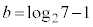 �̂Ƃ��ɁA
�̂Ƃ��ɁA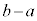 �́A
�́A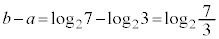 �ƂȂ�ŏ��ł��B
�ƂȂ�ŏ��ł��B (iii)�ł́A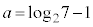 �C
�C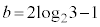 �̂Ƃ��ɁA
�̂Ƃ��ɁA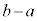 �́A
�́A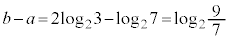 �ƂȂ�ŏ��ł��B
�ƂȂ�ŏ��ł��B (i)�C(ii)�C(iii)�̍ŏ��̏ꍇ���r�����(�ΐ������Q��)�A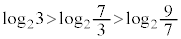 ���A
���A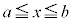 �ɂ�����
�ɂ�����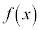 �̍ő�l��M�C�ŏ��l��m�ƂȂ�悤�Ȏ����̑g
�̍ő�l��M�C�ŏ��l��m�ƂȂ�悤�Ȏ����̑g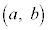 �̂����A
�̂����A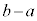 ���ŏ��ƂȂ�g�́A
���ŏ��ƂȂ�g�́A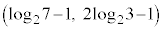 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2026(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B