���嗝�H���w'26�N[3]
���W��ԓ��ɓ_A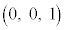 �CB
�CB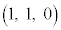 �C����ю���a��p���ĕ\�����_P
�C����ю���a��p���ĕ\�����_P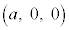 ���Ƃ�B����ɁA2�_
���Ƃ�B����ɁA2�_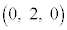 �C
�C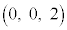 ��ʂ钼����
��ʂ钼����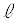 �Ƃ��āA3�_A�CB�CP����߂镽�ʂƒ���
�Ƃ��āA3�_A�CB�CP����߂镽�ʂƒ���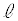 �Ƃ̌�_��Q�Ƃ���B
�Ƃ̌�_��Q�Ƃ���B
(1) �_Q�̍��W��a��p���ĕ\���B
(2) 4�_A�CB�CP�CQ���l�p�`APBQ�𐬂��A����AB�Ɛ���PQ������邽�߂�a�̏��������߂�B
(3) a��(2)�̏��������Ƃ��A�l�p�`ABPQ�̖ʐς�a��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��ԃx�N�g���̖��ł����A(2)�C(3)�͕��ʐ}�`�̖��Ƃ��ĉł��܂��B
3�_A�CB�CP����߂镽�ʂ�α�Ƃ��܂��Bu�Cv�������Ƃ��A
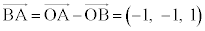 �C
�C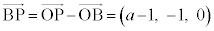 �@����@
�@����@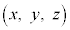 ��(���ʂ̃x�N�g�����������Q��)�A
��(���ʂ̃x�N�g�����������Q��)�A
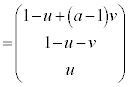 �@����A
�@����A
2�_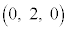 �C
�C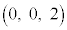 ��ʂ钼��
��ʂ钼��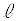 ��̓_
��̓_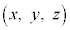 ���At �������Ƃ��A�����x�N�g��
���At �������Ƃ��A�����x�N�g��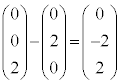 ��p����(�����̃x�N�g�����������Q��)�A
��p����(�����̃x�N�g�����������Q��)�A
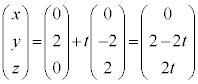 �@����B
�@����B
(1) ����α�ƒ���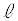 �̌�_Q�́A�A���B�Ƃ��āA
�̌�_Q�́A�A���B�Ƃ��āA �D�{�E���A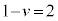 �@��
�@�� 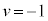 ����ƇE���C�ɑ�����A
����ƇE���C�ɑ�����A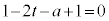 �@��
�@�� 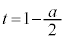 �E���A
�E���A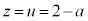
�D���A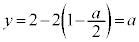
����āAQ�̍��W�́A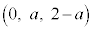 ......[��]
......[��]
A��z����̒�_�AP��x����̓_�AB��x����ɂ�z����ɂ����݂��Ȃ���_�̂ŁA3�_A�CB�CP���꒼����ɕ��Ԃ��Ƃ͂Ȃ��A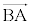 ��
��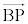 ��1���Ɨ��ł��B
��1���Ɨ��ł��B
Q�͕���α��̓_�ŁA����ȍ~�́A����α��̕��ʐ}�`�̖��ɂȂ�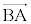 ��
��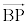 ��p���čl���Ă����܂��B�A���A
��p���čl���Ă����܂��B�A���A
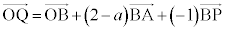
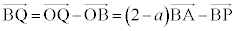 �@����F
�@����F
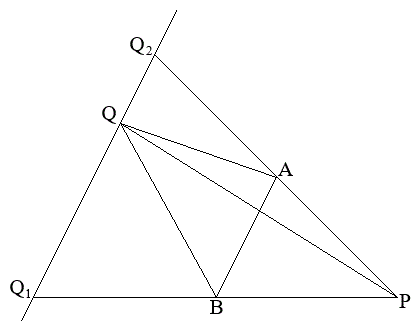 (2) �F��
(2) �F��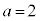 �Ƃ���ƁA
�Ƃ���ƁA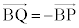 �ƂȂ�A����BP���B�ɑ���BP�Ɠ�����������P�Ƌt���̓_��
�ƂȂ�A����BP���B�ɑ���BP�Ɠ�����������P�Ƌt���̓_��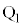 (
(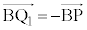 )�Ƃ��āAQ��
)�Ƃ��āAQ��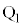 �ɗ��܂��B���̂Ƃ��́AB�CP�CQ���꒼����ɕ��Ԃ̂Ŏl�p�`APBQ�͂ł��܂���B
�ɗ��܂��B���̂Ƃ��́AB�CP�CQ���꒼����ɕ��Ԃ̂Ŏl�p�`APBQ�͂ł��܂���B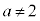 �̂Ƃ��A
�̂Ƃ��A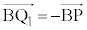 �ƇF��p����ƁA
�ƇF��p����ƁA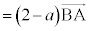 �@����G
�@����G�ƂȂ�̂ŁA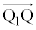 //
//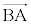 �ł��B�܂�AQ�́A
�ł��B�܂�AQ�́A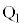 ��ʂ蒼��BA�ɕ��s�Ȓ�����̓_�ł��B���̒����ƒ���PA�̌�_��
��ʂ蒼��BA�ɕ��s�Ȓ�����̓_�ł��B���̒����ƒ���PA�̌�_��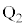 �Ƃ���ƁABA//
�Ƃ���ƁABA//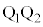 �Ȃ̂Œ��_�A���藝(
�Ȃ̂Œ��_�A���藝(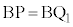 )���AA��
)���AA��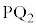 �̒��_�ŁA
�̒��_�ŁA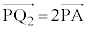 �ł��B�܂��A
�ł��B�܂��A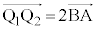 �ł��B�G��Q��
�ł��B�G��Q��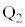 �ƍl����ƁA
�ƍl����ƁA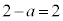 �@��
�@�� 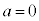 ���̂Ƃ����AA�CP�CQ���꒼����ɕ��Ԃ̂Ŏl�p�`APBQ�͂ł��܂���B
���̂Ƃ����AA�CP�CQ���꒼����ɕ��Ԃ̂Ŏl�p�`APBQ�͂ł��܂���B
�E�}���AQ������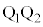 ��ɂ���A����AB�Ɛ���PQ�������܂��BQ������
��ɂ���A����AB�Ɛ���PQ�������܂��BQ������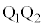 ��ɂ���Ƃ��A
��ɂ���Ƃ��A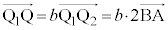 �Ƃ��āA
�Ƃ��āA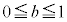 �ł��B�G���A
�ł��B�G���A ����āA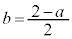
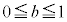 ���A
���A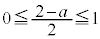 �@��
�@�� 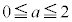
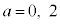 �̂Ƃ��͎l�p�`APBQ���ł����A
�̂Ƃ��͎l�p�`APBQ���ł����A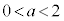 �ł���Ύl�p�`APBQ���ł���̂ŁA���߂�a�̏����́A
�ł���Ύl�p�`APBQ���ł���̂ŁA���߂�a�̏����́A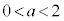 ......[��]
......[��]
(3) ��ABP�Ɓ�ABQ�ɂ����āA���_�A���藝���A�����͓������A��ӂ͂Ƃ���AB�Ȃ̂ŁA��ABP�̖ʐςƁ�ABQ�̖ʐς͓������A�l�p�`APBQ�̖ʐς́A��ABP�̖ʐς�2�{�ł��B��ABP���ʐ�S�́A �@���A
�� 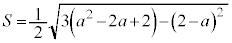
�l�p�`APBQ�̖ʐς͂���2�{�ŁA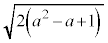 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2026(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 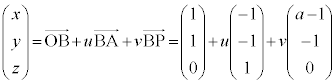
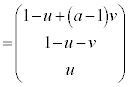 �@����A
�@����A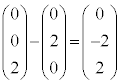 ��p����(�����̃x�N�g�����������Q��)�A
��p����(�����̃x�N�g�����������Q��)�A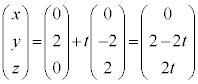 �@����B
�@����B