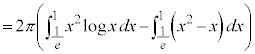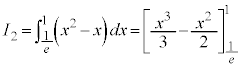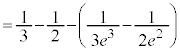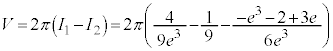���嗝�H���w'26�N[5]
��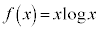 �ɂ��āA�ȉ��̖�ɓ�����B�������A
�ɂ��āA�ȉ��̖�ɓ�����B�������A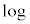 �͎��R�ΐ��Ae�͎��R�ΐ��̒��\���B�K�v�Ȃ�A
�͎��R�ΐ��Ae�͎��R�ΐ��̒��\���B�K�v�Ȃ�A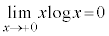 ��p���Ă悢�B
��p���Ă悢�B
(1) 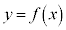 �̑����A�ɒl�ׂāA���̃O���t�������B
�̑����A�ɒl�ׂāA���̃O���t�������B (2) ����a�ɑ��āA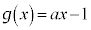 �Ƃ���B�Ȑ�
�Ƃ���B�Ȑ�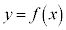 �ƒ���
�ƒ���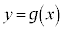 �̋��L�_�̌��́Aa�̒l�ɂ���Ăǂ̂悤�ɕς�邩���ׂ�B
�̋��L�_�̌��́Aa�̒l�ɂ���Ăǂ̂悤�ɕς�邩���ׂ�B (3) �Ȑ�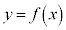 �ƒ���
�ƒ���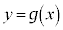 �̋��L�_�̌���1�̂Ƃ��A�Ȑ�
�̋��L�_�̌���1�̂Ƃ��A�Ȑ�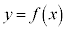 �C����
�C����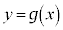 ����ђ���
����ђ���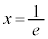 �ň͂܂ꂽ������y���̎����1��]�����Ăł��闧�̂̑̐ς����߂�B
�ň͂܂ꂽ������y���̎����1��]�����Ăł��闧�̂̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���̖��́A�����E�ϕ��̊�{���Ȃ̂ŗ��Ƃ��܂���B�v�Z�~�X�ɂ͂��ꂮ������ӂ��Ă��������B
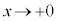 �̂Ƃ��A
�̂Ƃ��A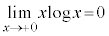 ���A
���A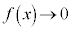
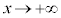 �̂Ƃ��A
�̂Ƃ��A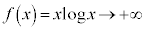
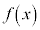 �������\�͈ȉ��̂悤�ɂȂ�܂��B
�������\�͈ȉ��̂悤�ɂȂ�܂��B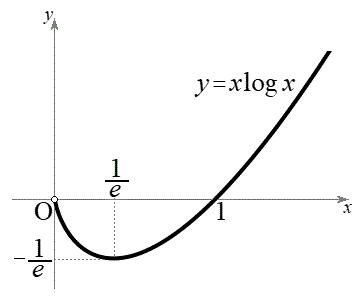
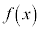 ��
��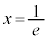 �ɂ����ċɏ��l
�ɂ����ċɏ��l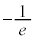 ���Ƃ�܂��B
���Ƃ�܂��B
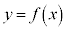 �̃O���t�͉E�}�B
�̃O���t�͉E�}�B
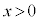 �Ȃ̂ŁA
�Ȃ̂ŁA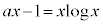
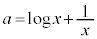 �@����B
�@����B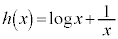 �Ƃ����ƁA
�Ƃ����ƁA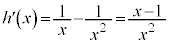
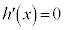 �Ƃ���ƁA
�Ƃ���ƁA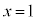
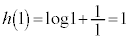
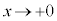 �̂Ƃ��A
�̂Ƃ��A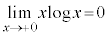 ���A
���A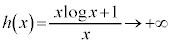
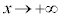 �̂Ƃ��A
�̂Ƃ��A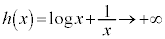
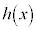 �̑����\�͈ȉ��̂悤�ɂȂ�܂��B
�̑����\�͈ȉ��̂悤�ɂȂ�܂��B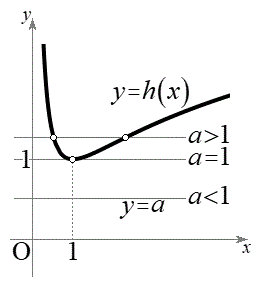 ������A
������A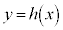 �̃O���t�͉E�}�̂悤�ɂȂ�܂��B
�̃O���t�͉E�}�̂悤�ɂȂ�܂��B
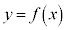 ��
��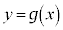 ��A�������Ƃ��̉��́A
��A�������Ƃ��̉��́A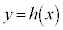 ��
��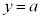 ��A�������Ƃ��̉��Ɉ�v����̂ŁA
��A�������Ƃ��̉��Ɉ�v����̂ŁA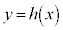 �̃O���t���A�Ȑ�
�̃O���t���A�Ȑ�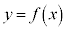 �ƒ���
�ƒ���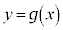 �̋��L�_�̌��́A
�̋��L�_�̌��́A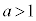 �̂Ƃ�2�A
�̂Ƃ�2�A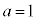 �̂Ƃ�1�A
�̂Ƃ�1�A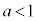 �̂Ƃ�0�� ......[��]
�̂Ƃ�0�� ......[��]
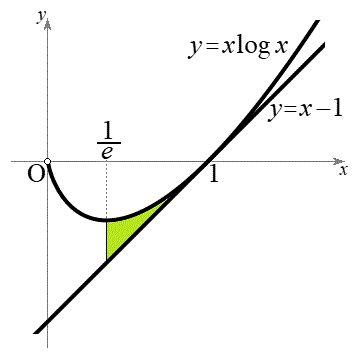 (3) (2)���A�Ȑ�
(3) (2)���A�Ȑ�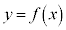 �ƒ���
�ƒ���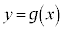 �̋��L�_�̌���1�̂Ƃ��A
�̋��L�_�̌���1�̂Ƃ��A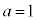 �ł��B���̂Ƃ��A
�ł��B���̂Ƃ��A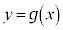 �́A
�́A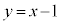 �ƂȂ�A
�ƂȂ�A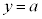 ��
��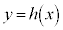 �̋��L�_�A����
�̋��L�_�A����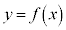 ��
��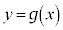 �̋��L�_��
�̋��L�_��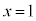 �ŁA������
�ŁA������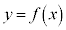 ��
��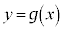 �͐ڂ��܂��B
�͐ڂ��܂��B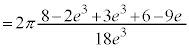
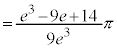 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2026(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B