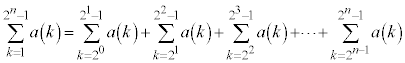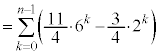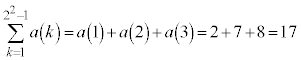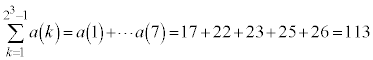���嗝�H���w'26�N[4]
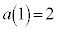 �Ƃ��A
�Ƃ��A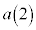 �C
�C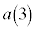 �C
�C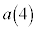 �C��������̊W�Œ�߂�B
�C��������̊W�Œ�߂�B
�ȉ��̖�ɓ�����B
(1) 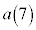 �C
�C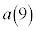 �����߂�B
�����߂�B (2) ���R��n�ɑ��āA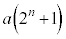 �́A1�܂���2�̂����ꂩ�̒l���Ƃ�悤��
�́A1�܂���2�̂����ꂩ�̒l���Ƃ�悤��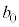 �C
�C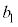 �C����C
�C����C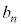 ��p���āA
��p���āA �ƕ\����B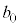 �C
�C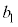 �C����C
�C����C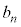 �����ꂼ�ꋁ�߂�B
�����ꂼ�ꋁ�߂�B (3) ���R��n�ɑ��āA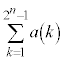 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ł��B(2)��(3)�̃q���g�ɂȂ��Ă���̂��낤�A�Ɣ��z����Ƃ��܂��s���܂���B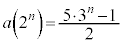 ��
��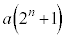 �����߂��Ă�(
�����߂��Ă�(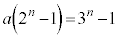 �����߂��܂���)�A
�����߂��܂���)�A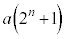 ��
��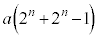 (
(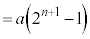 )�̊Ԃ�������܂���B
)�̊Ԃ�������܂���B
�@��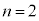 �Ƃ���ƁA
�Ƃ���ƁA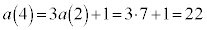 �C
�C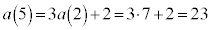
�@��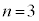 �Ƃ���ƁA
�Ƃ���ƁA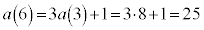 �C
�C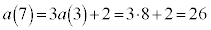
�@��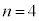 �Ƃ���ƁA
�Ƃ���ƁA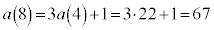 �C
�C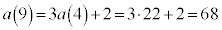
����āA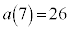 �C
�C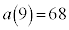 ......[��]
......[��]
(2) 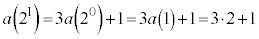 �C
�C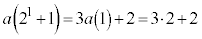 �@����A
�@����A �Ƃ���Ă����ƁA
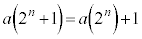 �C
�C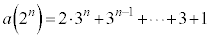 �@���(��)
�@���(��)�Ɨ\���ł��܂��B
������܂��ؖ����܂��B
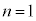 �̂Ƃ��A�A��萬�藧���܂��B
�̂Ƃ��A�A��萬�藧���܂��B
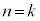 �̂Ƃ��A(��)����������Ɖ��肵�܂��B
�̂Ƃ��A(��)����������Ɖ��肵�܂��B 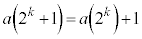 �C
�C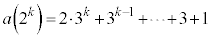 �@����B
�@����B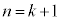 �̂Ƃ��A
�̂Ƃ��A�@��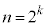 �Ƃ���ƁA�B��p���āA
�Ƃ���ƁA�B��p���āA ���A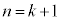 �̂Ƃ���(��)���������܂��B
�̂Ƃ���(��)���������܂��B ���w�I�A�[�@�ɂ��A���ׂĂ̎��R��n�ɂ��āA(��)���������܂��B(��)���A ����āA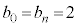 �C
�C ......[��]
......[��]
(3) (2)���ǂ�����Ďg���̂��낤�A�ƁA�܂��l����Ǝv���܂����A(2)�Ɠ��l�̂��Ƃ�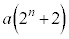 �C
�C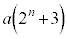 �C
�C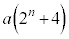 �C����ɂ��Ă�낤�Ƃ���ƁA
�C����ɂ��Ă�낤�Ƃ���ƁA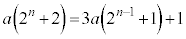 �C
�C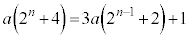 �C����̂ł������o���o���Ŕj�]���܂��B
�C����̂ł������o���o���Ŕj�]���܂��B �����ŁA��蕶����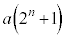 ��
��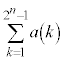 (���̌������Q��)��
(���̌������Q��)��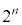 ���q���g�Ƃ��čl���܂��B��ɂ��������悤�ɁA
���q���g�Ƃ��čl���܂��B��ɂ��������悤�ɁA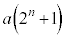 ��
��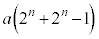 (
(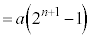 )�̊Ԃ�������ׂĂ�������Ȃ��̂ŁA
)�̊Ԃ�������ׂĂ�������Ȃ��̂ŁA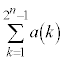 �̒�������ɕ����Ă܂Ƃ߂邱�Ƃ��l���܂��B�܂Ƃ߂�Ƃ���ƁA
�̒�������ɕ����Ă܂Ƃ߂邱�Ƃ��l���܂��B�܂Ƃ߂�Ƃ���ƁA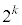 �C
�C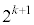 �ŋ���āA
�ŋ���āA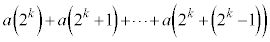 ���ǂ��Ȃ��Ă��邩�ׁA��ŁA���̘a�����߂�悢�A�Ƃ������ƂɂȂ�܂��B
���ǂ��Ȃ��Ă��邩�ׁA��ŁA���̘a�����߂�悢�A�Ƃ������ƂɂȂ�܂��B
�Ⴆ�A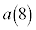 ����
����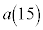 �܂ł��l����ƁA
�܂ł��l����ƁA �����̘a���l����ƁA
�ɂȂ��Ă��܂��B����ŁA�Q��������ꂻ���ł��B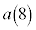 ����
����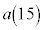 �܂ł̘a��
�܂ł̘a��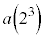 ����
����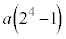 �܂ł̘a�ł���A
�܂ł̘a�ł���A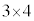 ��4�́A
��4�́A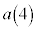 ����
����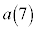 �܂ł̍���
�܂ł̍���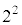 �ł��B
�ł��B
�����ŁA 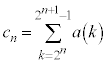 �@����C
�@����C�Ƃ���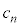 �̑Q���������܂��B
�̑Q���������܂��B 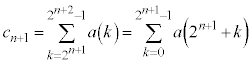 �@(
�@(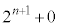 �Ԗڂ���
�Ԗڂ���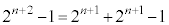 �Ԗڂ̘a���l���Ă���)
�Ԗڂ̘a���l���Ă���)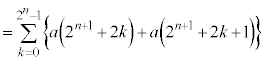 �@(2�����̑g�ōl���A�����ԖڂƊ�Ԗڂɕ�����)
�@(2�����̑g�ōl���A�����ԖڂƊ�Ԗڂɕ�����)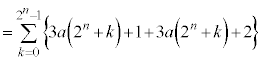 �@(�� �@��n��
�@(�� �@��n��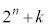 �Ƃ���)
�Ƃ���)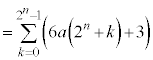
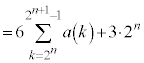 �@(
�@(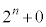 �Ԗڂ���
�Ԗڂ���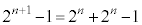 �Ԗڂ̘a���l���Ă���)
�Ԗڂ̘a���l���Ă���)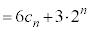
���D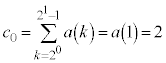 �������ƍl���邱�Ƃ��ł��܂��B
�������ƍl���邱�Ƃ��ł��܂��B �D�̗��ӂ�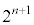 �Ŋ���ƁA
�Ŋ���ƁA 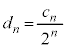 �Ƃ����āA
�Ƃ����āA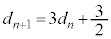 �@����E
�@����E
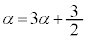 �@����F
�@����F�Ƃ���ƁA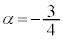
�E�|�F���A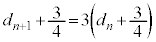
����āA����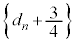 �́A����3�C����
�́A����3�C����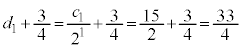 �����䐔���ł��B
�����䐔���ł��B 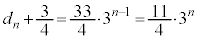 �C
�C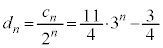
�� 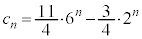 �@����G
�@����G
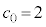 �Ȃ̂ŁA�G��
�Ȃ̂ŁA�G��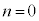 �ł����藧���܂��B
�ł����藧���܂��B
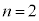 �Ƃ��Ċm���߂�ƁA
�Ƃ��Ċm���߂�ƁA �G�ł́A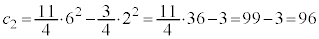
�C��p���āA���߂�a�́A ���D�m���߂Ă݂܂��B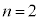 �̂Ƃ��A
�̂Ƃ��A 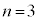 �̂Ƃ��A
�̂Ƃ��A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2026(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 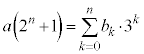
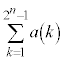 �����߂�B
�����߂�B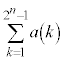 (���̌������Q��)��
(���̌������Q��)��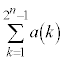 �̒�������ɕ����Ă܂Ƃ߂邱�Ƃ��l���܂��B�܂Ƃ߂�Ƃ���ƁA
�̒�������ɕ����Ă܂Ƃ߂邱�Ƃ��l���܂��B�܂Ƃ߂�Ƃ���ƁA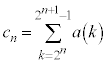 �@����C
�@����C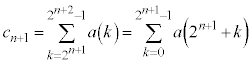 �@(
�@(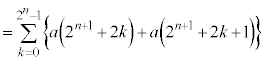 �@(2�����̑g�ōl���A�����ԖڂƊ�Ԗڂɕ�����)
�@(2�����̑g�ōl���A�����ԖڂƊ�Ԗڂɕ�����)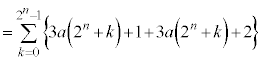 �@(�� �@��n��
�@(�� �@��n��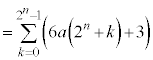
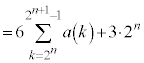 �@(
�@(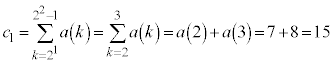
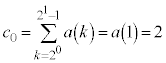 �������ƍl���邱�Ƃ��ł��܂��B
�������ƍl���邱�Ƃ��ł��܂��B