���K'08�N[20]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
(3���ԑQ����) ����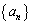 ��
��
���݂����Ƃ��A���̖₢�ɓ�����B
(1) x��2����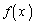 �ŁA
�ŁA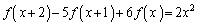 ���݂������̂����߂�B
���݂������̂����߂�B (2) 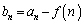 �Ƃ����Ƃ��A����
�Ƃ����Ƃ��A����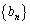 �̈�ʍ������߂�B
�̈�ʍ������߂�B (3) ����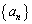 �̈�ʍ������߂�B
�̈�ʍ������߂�B (4) 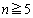 �̂Ƃ��A
�̂Ƃ��A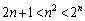 �𐔊w�I�A�[�@�Ŏ����B
�𐔊w�I�A�[�@�Ŏ����B (5) 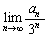 �����߂�B
�����߂�B (���m��'08)
���@(4)�����w�I�A�[�@���Q�Ƃ��Ă��������B
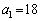 �C
�C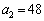 �C
�C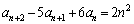 �@����@
�@����@
(1) 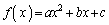 �Ƃ����B
�Ƃ����B 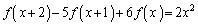 �@����A
�@����A�ƂȂ邽�߂ɁA�W�����r���āA
(2) 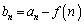 �Ƃ����ƁA
�Ƃ����ƁA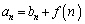
�@�ɑ������ƁA
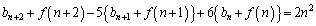 �@����B
�@����B�A��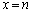 �Ƃ��āA
�Ƃ��āA ������B�́A
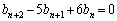 �@����C�@(3���ԑQ�������Q��)�C�̓����������F
�@����C�@(3���ԑQ�������Q��)�C�̓����������F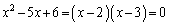 ���A
���A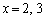
������A
�C �� 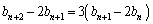
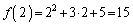 �C
�C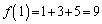 ���A
���A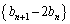 �́A����
�́A����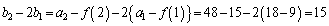 �C����3�����䐔���B
�C����3�����䐔���B
�� 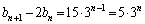 �@����D
�@����D
�܂��A
�C �� 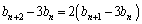
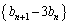 �́A����
�́A����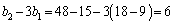 �C����2�̓��䐔��B
�C����2�̓��䐔��B
�� 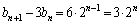 �@����E
�@����E
�D�|�E���A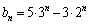 ......[��]
......[��]
(3) 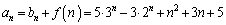 ......[��]
......[��]
(4) (�T) 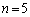 �̂Ƃ��A
�̂Ƃ��A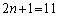 �C
�C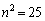 �C
�C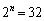 ���A
���A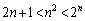 �����藧���܂��B
�����藧���܂��B (�U) 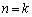 �̂Ƃ��A
�̂Ƃ��A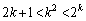 �@����F�@�����藧�Ɖ��肵�܂��B
�@����F�@�����藧�Ɖ��肵�܂��B �F�̊e�ӂ�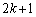 ��������ƁA
��������ƁA 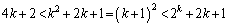 �@����G
�@����G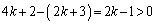 (
(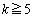 )���A
)���A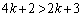 �@����H
�@����H
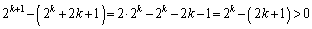 �@(�� �F)
�@(�� �F)�� 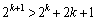 �@����I
�@����I
�G�C�H�C�I���A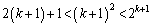
����āA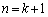 �̂Ƃ��ɂ����藧���܂��B
�̂Ƃ��ɂ����藧���܂��B (�T)�C(�U)���A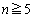 �̂Ƃ��A
�̂Ƃ��A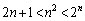 �����藧���܂��B
�����藧���܂��B
(5) (4)�̌��ʂɂ��A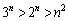 ���A
���A ����āA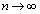 �̂Ƃ��A
�̂Ƃ��A �� 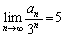 .......[��]
.......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B