�K�E�X�̖@���̈�ʉ�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�Ȗ�U�ň͂܂ꂽ�̈�����d��Q�����݂���Ƃ��A�Ȗʏ�ɂ������d�E��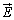 �Ƃ��āA
�Ƃ��āA
�K�E�X�̖@���F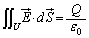
����������B
�^�Ō��_O���d��Q���u����Ă���Ƃ��A���_O�����͂ޔC�ӂ̕Ȗ�U�ɂ��āA�Ȗʏ�̊e�_�ɂ������d�E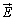 ���ʐϕ����l���܂��B
���ʐϕ����l���܂��B
�]���āA���ʏ�ōl�����K�E�X�̖@���F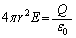 �C�����A�d��Q�����͂ދ��ʂ�ʉ߂����d�C�͐��̖{����
�C�����A�d��Q�����͂ދ��ʂ�ʉ߂����d�C�͐��̖{����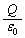 �{�ɂȂ�A�Ƃ����@���́A�C�ӂ̓ʂȕȖ�U�ɂ����Ă����藧���܂��B
�{�ɂȂ�A�Ƃ����@���́A�C�ӂ̓ʂȕȖ�U�ɂ����Ă����藧���܂��B
�Ȗʏ�̊e�_���d�E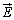 ����l�ł��Ȗʂ̐ڕ��ʂɐ����ł���ꍇ�ɂ́A�Ȗʂ��ʐ���S�Ƃ��āA
����l�ł��Ȗʂ̐ڕ��ʂɐ����ł���ꍇ�ɂ́A�Ȗʂ��ʐ���S�Ƃ��āA
������A
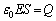 �@����@
�@����@
�d��Q����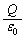 �{���d�C�͐����o��̂ł����A�d��Q����Q�{�̐������т�̂��ƍl�������̂��d���ƌ����܂��B�P�ʖʐϓ�������d�����d�����x�ƌ����܂��B�^�ł́A�d�����x
�{���d�C�͐����o��̂ł����A�d��Q����Q�{�̐������т�̂��ƍl�������̂��d���ƌ����܂��B�P�ʖʐϓ�������d�����d�����x�ƌ����܂��B�^�ł́A�d�����x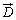 ���d�E
���d�E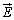 �Ƃ̊Ԃɂ́A
�Ƃ̊Ԃɂ́A
�Ƃ����W������܂�
�^��̗U�d��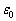 �̒P�ʂ�
�̒P�ʂ�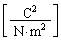 �C�d�E
�C�d�E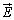 �̒P�ʂ�[N/C]�Ȃ̂ŁA�d�����x
�̒P�ʂ�[N/C]�Ȃ̂ŁA�d�����x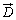 �̒P�ʂ́A
�̒P�ʂ́A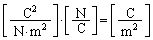 �C�d���̒P�ʂ�[C](�d�ׂƓ���)�ƂȂ�܂��B
�C�d���̒P�ʂ�[C](�d�ׂƓ���)�ƂȂ�܂��B
�d�����x�̑傫��D��p����ƁA�����@�́A
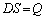 �@(�d��DS���d��Q�ɓ������Ɗo���܂�)
�@(�d��DS���d��Q�ɓ������Ɗo���܂�)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@������b����TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B